Introduction

Flow and heat transfer within the rotating cavities that are formed between successive rotor discs in axial compressors is an important topic of research concerning gas turbine engines. The radial growth of these discs control the running tip clearance of the compressor blades which in turn determine the range and the aerodynamic performance of the compressor. With the regulatory bodies tightening the emission standards there is a quest for ultra-high bypass ratio engines with smaller core diameters that provide higher propulsive efficiency. The tip clearance control is more important than ever in these smaller core engines and there is a need to better understand and model the complicated aerothermal mechanisms that control the flow structure and the heat transfer in these cavities. The coupled nature of the buoyancy driven cavity internal flow development and the disc heat transfer, its interaction with the colder throughflow air along the shaft bore, all make it highly inaccessible for experimentation and even less amenable to numerical simulation employing modelled turbulence.

A number of researchers have contributed to our current understanding of the flow physics associated to rotating cavities within axial compressors. A set of dimensionless parameters have been traditionally used by such researchers for characterising the conditions within a rotating cavity with axial throughflow. These parameters are also used to describe the flow regimes in the current work and are therefore presented first in Table 1.

Flow visualisation and LDA measurements in three different flow geometries were reported by Pincombe (1983). These included a cavity with a central axial throughflow, a cavity with a radial outflow and a cavity with radial inflow. Two modes of breakdown were observed for both laminar and turbulent flow in a cavity with axial throughflow. An asymmetric spiral breakdown was observed where the axial jet departed from the central axis and proceeded violently inside the cavity. An axisymmetric breakdown was observed when the axial jet extended inside the cavity. It was also found that the boundaries between the different breakdown modes were dependent upon the Rossby number. Firouzian et al. (1985) conducted flow visualisation in a rotating cavity with a radial inflow. The rotational Reynolds number tested was up toReθ≈106. The inner to outer radius ratio (a/b) was 0.1 and the gap ratio that is the ratio of disc axial spacing to cavity outer radii (G=s/b) was 0.133. The authors used five different shroud geometries in their tests and found that there is a source region near the shroud, laminar or turbulent Ekman layers on the discs, an interior core of fluid near the centre of the cavity as well as a sink layer. The authors also reported that above a certain flow rate, this structure tended to be unstable and the flow tended to stabilise when heating one of the discs. Owen et al. (1985) formulated the linear equations of inviscid rotating fluid and made a comparison between the theory and the available experimental data. LDA measurement were conducted in the interior core between the Ekman layers with a radial outflow or inflow of air in a number of rotating cavity rigs. There was good agreement between the measurements and the theoretical models over a wide range of flow rates, rotational Reynolds numbers and radial locations. Farthing et al. (1992a) conducted flow visualisation and LDA measurement to study the flow structure in isothermal and heated rotating cavities using four different rigs. The axial Reynolds number for all their experiments (Rez) was constant. They showed that for a stationary cavity where the gap ratio (G) is above 4 and the Rossby number (Ro) is infinite, a strong toroidal vortex is generated by the bore flow migrating inside the cavity. The authors proposed a model of the non-axisymmetric flow structure within the cavity as shown schematically in Figure 1. The model described cold throughflow air penetrating the cavity radially outwards in a ‘radial arm’. The radial arm then formed a pair of vortical structures with opposite sense of rotation. The region that rotated in the same direction as the disc was termed ‘cyclonic’ and the one that rotated in the opposite direction to the disc was termed ‘anticyclonic’. The cyclonic and anticyclonic circulations where identified with low and high reduced static pressures (P∗) respectively. The two vortex regions were separated by a ‘dead’ zone corresponding to where the flow left the cavity radially inwards in Ekman layers. This model has been subsequently used by many researchers to describe the prevailing flow structure in a heated rotating cavity.

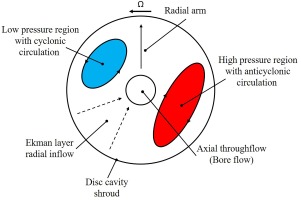
Figure 1.

Schematic of flow structure in heated rotating cavity with axial throughflow of cooling air (Based on the model proposed in Farthing et al., 1992a).

Bohn et al. (2000) conducted flow visualisation within a rotating cavity and reported a similar flow structure as Farthing et al. (1992a). The role of buoyancy on heat transfer in rotating cavities was the focus of Alexiou (2000) whose measurements revealed that the flow in rotating cavities can be dominated by free convection, forced convection or both (Alexiou et al., 2000; Long et al., 2003). Owen and Powell (2004) carried out LDA and heat transfer measurements in a single cavity rig, with a/b ≈ 0.4 and G≈0.2 where the downstream disc was heated. A spectral analysis of the LDA measurements revealed a multi-cell structure including up to three pairs of cyclonic and anticyclonic vortices in the flow field. They also found that although there are some exceptions, the number of pairs of cyclonic and anticyclonic vortices was reduced by increasing the rotational Reynolds number at a constant axial Reynold number. Long et al. (2007) conducted LDA measurements inside a heated multiple cavity (consisting of 4 cavities and 5 discs) with axial throughflow where a/b ≈ 0.318 and G≈0.195 for each cavity. The shroud, in their rig, was heated by an external flow of hot air within a pressurised outer casing. The LDA system measured the velocities in cavities 3 and 4 whereas temperatures were measured along the walls of cavities 2 and 3 by a limited number of embedded thermocouples. The frequency spectrum obtained (Figure 2) from tangential velocity data for mid-plane of cavity 3 at radial location of r/b ≈ 0.765 showed the evidence of the dominant frequency at approximately twice that of the rotational speed of the flow implying the presence of two vortex pairs around that specific location.

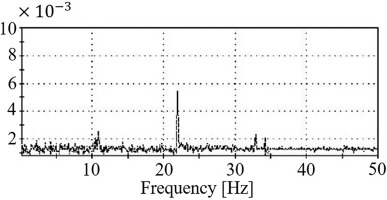
Figure 2.

Spectral analysis of the tangential component of velocity, (rotational speed of cavity = 10.92 Hz), from (Long et al., 2007).

Dweik et al. (2009b) conducted a total of fifteen unsteady computational case studies for an open rotating cavity for idle, high-power and shutdown conditions. The test rig conditions in Owen and Powell (2004) was imitated to develop a numerical test case. The data showed a temporal evolution in flow structure eventually resulting in the formation of the radial arms. The results from the test cases showed a consistent agreement with the data from Johnson et al. (2006). The above authors also showed that despite the unstable and evolutionary nature of the complicated flow pattern, the free convection correlations for a vertical flat plate with constant temperature gives an encouraging prediction for the global Nusselt number values for the buoyancy-induced flow (Dweik et al., 2009a). Atkins and Kanjirakkad (2014) conducted measurements in the same multiple cavity rig as (Alexiou, 2000; Long et al., 2007) but this time with a stationary shaft and the direction of flow through the rig reversed compared to the previous builds. Additionally, in these experiments the shroud was radiantly heated. They measured the steady state temperatures on both sides of the disc separating cavities 2 and 3 that was instrumented by embedded surface thermocouples. The results demonstrated the sensitivity of the radial temperature distributions along the disc with the variation of Grashof number, axial throughflow and rotational Reynolds number for approximately constant Rossby number. For instance, for Ro≈5 and a rotational Reynolds number of Reθ=8×104 there existed an almost linear dimensionless temperature profile from r/b≈0.4−0.9. The results also showed that for low Rossby numbers (Ro≤1) and large Grashof numbers, where the buoyancy effects are expected to dominate, the Nusselt number (Nu) increased with increasing Gr. Owen and Long (2015) published a comprehensive review of buoyancy induced flow in both closed and open rotating cavities with either axial throughflow or a radial inflow of air. Amirante et al. (Amirante et al., 2016) conducted a computational study based on the thermal data from (Atkins, 2013). Although there was a qualitative agreement with the measurements, the disc temperatures were considerably over-predicted due to an under-predication of the axial throughflow penetration into the cavity.

In this paper, the authors present experimental data obtained from the Sussex Multiple Cavity Rig (MCR) for a fixed rotational Reynolds number (Reθ) of 7.1 × 10⁵ at three different axial Reynolds numbers (Rez); 1.2, 2.4 and 4.8 × 10⁴ (and Ro; 0.32, 0.64 and 1.28). These will be referred to as cases 1, 2 & 3 respectively in the subsequent discussions. The condition corresponding to case-2 has been simulated numerically and the results are presented and compared with experimental data. The paper also discusses the sensitivity of the flow structure to variations in Rossby number (Ro) and buoyancy parameter (βΔT) for the flow conditions as mentioned above. The buoyancy parameter is defined as:

where, β is the coefficient of volume expansion such that β=1/Tin and Tin is air temperature at the bore in the middle of the cavity. ΔT is the difference between the shroud metal temperature (Tsh) and the cavity inlet air temperature. The locations of air and metal temperature thermocouples inside the cavity 3 are shown in Figure 3.

Figure 3.

Distribution of thermocouples in cavity 3.

Research methodology

The Sussex Multiple Cavity Rig (MCR) is used to study the heat transfer dominated flow structure within the multiple rotating cavities that are typical of an aero-engine high pressure compressor. The current rig is a 70% scaled replica of a typical high pressure compressor internal air system.

Experimental set up

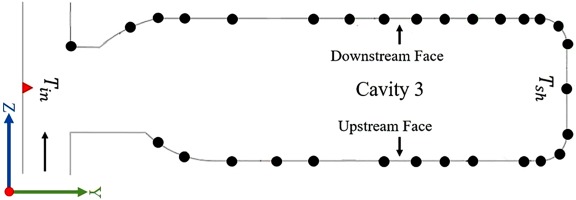
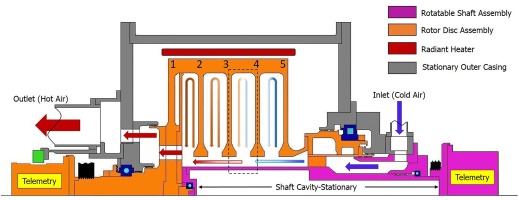
There have been several modification on the MCR over the years. Figure 4 illustrates the cross-sectional view of the rig in its current configuration. The pink sections illustrates the new stationary shaft where the LDA window is located. The grey region indicates the outer drum and other stationary components. The orange section is the rotating assembly and the red part represents the radiant heater array. The shaft telemetry that is stationary is shown in the purple region while the rotating rotor telemetry is presented in the orange region and located at the end of the rig. It is worth noting that the direction of the axial throughflow (cold air) is in the opposite direction to the disc and cavity numbering. The cavity discussed in this paper is the cavity 3 that is located between discs 3 and 4 (dashed black rectangle).

Figure 4.

Cross-sectional view of the MCR.

The rotating assembly is manufactured from Ti-6Al-4V titanium alloy. The inner radius (a) and the outer radius (b) of the cavities are 70.1 and 220 mm respectively, hence the radius ratio (a/b) is 0.318. The disc spacing (s) is 42.9 mm and the gap ratio (G) is 0.195. The central shaft radius (r_s) is 52 mm and the hydraulic diameter (d_h) is 36.2 mm. The shaft is held stationary for all runs. The air passes between six rotating blocks (rectangular, 10 mm wide) before entering the bore region in order to form a similar flow restriction to the rotor endplate. A two stage, screw type, Atlas Copco ZT250 compressor was used to supply the throughflow air. The mass flow rate was measured by a calibrated venturi meter installed in the inlet pipe work upstream of the rig. An array of radiant heaters (red section) is positioned circumferentially around the outer casing to simulate the hot flow in the annulus of the high pressure compressor. The rotational speed is measured by a magnetic pickup probe. Glass fibre insulated K-type thermocouples with wire dimeter of 0.25 mm were used to measure the temperature in the rotating frame of reference. The thermocouples are embedded circumferentially along a line for at least ten wire diameters to reduce the conduction errors. The nominal diameter of the thermocouple beads is 0.4 mm. The installation procedure is described in Atkins and Kanjirakkad (2014). The shaft air thermocouples are positioned at r/b = 0.25. The distribution of the thermocouples in the cavity was shown earlier in Figure 3. A comprehensive discussion of the experimental apparatus and measuring technique is provided by Fazeli et al. (2020).

LDA information

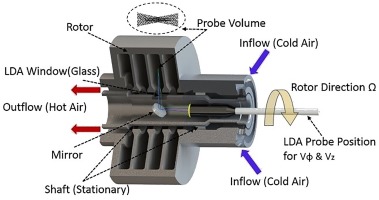
Laser Doppler Anemometry (LDA) was used to measure velocity components in the cavities and the bore region within the Multiple Cavity Rig. LDA has the advantage that the output burst signal is a function of velocity that does not need calibration. It can also detect reverse flows regions with a suitable frequency shifting technique. Figure 5 shows a cut-away of the LDA arrangement. The LDA systems uses a green colour beam with 514.3 nm wavelength and a blue colour beam with 488.3 nm wavelength each at power output of up to 1 Watt. The front optics (lens) has a choice of either a 100 mm or a 250 mm focal length to enable access to various radial measurement locations. As the lens with 250 mm focal length produces a 4 mm long probe volume its spatial resolution is unsuitable for near wall measurements in the shroud and particularly in the bore region. To overcome this, a lens with 100 mm focal length is used to measure in these regions. A Dantec 9010 six-jet atomiser using olive oil is employed to produce 1 µm diameter seeding particles. The optical access window is made of BK7 optical grade glass treated with an anti-reflection coating for the 480–520 nm wavelength range. As seen in Figure 5, the incident laser beams and reflected signals are diverted onto the probe using a 45° mirror located on the centre line of the rig. A traverse system consisting of two concentric tubes is used to move the probe volume inside the rig, one for moving the laser probe axially in relation the mirror and the other to move the mirror itself. The lens with the shorter focal length is used for measurements in the bore and the lower radius regions of the cavity whereas the longer focal length lens is employed for measurements in the outer cavity. The accuracy of placement of the axial and radial locations is considered to be ±0.5 mm.

Figure 5.

Cut-away view of the LDA probe positioning inside the MCR rig.

Numerical set up

Unsteady Reynolds Averaged Navier-Stokes (URANS) simulation of the flow filed in the rotating cavities is carried out using Ansys Fluent 19.1 in order to help the understanding of the cavity flow structure. The entire upstream flow domain with the first two successive cavities were simulated. ICEM-CFD 17.1 was used to generate a high resolution 2D multi-block mesh. A complete 3D domain for each cavity was made by revolving the 2D grid over 360 degrees in the circumferential direction around the rig axis. Each cavity domain includes around 9 million nodes. In order to have a high resolution within the boundary layers the method employed by Dweik et al. (2009b) is used to create 25 points in the first 2 mm normal to the wall with the first point located 0.005 mm away from the walls. A logarithmic bunching algorithm with a growth ratio of 1.1 is then used to reach a high resolution boundary layer resulting in a y⁺ < 1 on the cavity walls and shroud region. The meridional view of the computational domain within a cavity is shown in Figure 6. The turbulence model used was the k−ω SST model that combines both k−ε and k−ω models and benefits from automatic near wall treatment that switches to low-Reynolds number formulation in the viscous sub-layer (Dweik et al., 2009b). The converged steady-state results were used to kick-start the transient simulations presented in this paper. The experimental thermal data was used for the wall boundary condition on the shaft surface and all cavity walls. The experimental data was recorded at 3 Hz and the temperatures were averaged over a minute (180 samples) from thermally steady state conditions. This can help to reduce stochastic differences. The total pressure at the inlet boundary and the static pressure at the outlet are applied to match the experimental mass flow rate. The Boussinesq approximation was also used to accommodate buoyancy effects. The numerical time-step of the transient simulations is equivalent to 1° of rotation and the solution was run for 45 complete revolutions. Convergence of each time-step was completed when the equation residuals reached below1×10−4. A total of 22 days were required for the solution using 60 CPUs on the University of Sussex High Performance Computer. The non-dimensional parameters for the run is as follows:Ro=0.64,Reθ=7.1×105, Rez=2.4×104and βΔT=0.55. This corresponded to case-2 of the experimentation.

Figure 6.

Meridional plane of the numerical grid.

Results and discussion

As mentioned previously, this paper focuses on data acquired at a constant rotational Reynolds number (Reθ) of 7.1 × 10⁵. In the Sussex Multiple Cavity Rig, this corresponds to a rotational speed (Ω) of 2,000 rpm. The results of the spectral analysis conducted on the LDA data and the variation of the swirl value against the transient βΔT are discussed in the following sections. All the experimental data presented in this paper are obtained from steady state thermal conditions. The steady state mode was achieved once the variation of the temperatures shown by the thermocouples are less than 0.2 K within 5 min. It should also be noted that the LDA results discussed in this paper are the time-averaged results.

Spectral analysis of the LDA tangential component of velocity

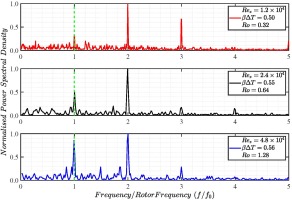
It was noted previously that Farthing et al. (1992a) provided evidence of the existence of a pair of vortices in a heated rotating cavity with axial throughflow by flow visualisation. Long et al. (2007) used frequency spectra analysis of the tangential velocity component obtained from LDA to detect the existence of vortex pairs in their study. In this paper, a similar power spectral density method is used for the identification of vortex pairs that may be present in the cavity flow field. The power spectral density is achieved by calculating the raw tangential velocity data by using a Fast Fourier Transform (FFT) technique. The averaged value of over 4,000 raw velocity samples that are equally spaced in time provide a measured value. To achieve this, sample/hold and resampling of the instantaneous data is carried out before the actual FFT analysis. The frequency spectra are presented for the conditions represented by cases 1 to 3 as mentioned above. The analysis were carried out in the mid plane (z/s = 0.5) of cavity 3 at two radial locations of r/b = 0.86 and 0.91.

Figures 7 and 8 shows the normalised power spectral density of the tangential velocity component in the mid plane of cavity 3 at the radial locations of r/b = 0.91 and 0.86 respectively. For each case, the LDA data at the two radial locations were measured with a fixed time interval between them such that the signal at the higher radius is acquired first followed by that at the lower radius (15 s later). The symbol f0 represents the rig rotational frequency that is approximately 33.25 Hz. The spike, which appears in each case, equals 3f0, in other words three times the frequency of solid body rotation.

Figure 7.

Measured frequency spectrum obtained from tangential velocity in the mid plane of cavity 3 at a radial location of r/b = 0.91 (Ω = 33.25 Hz).

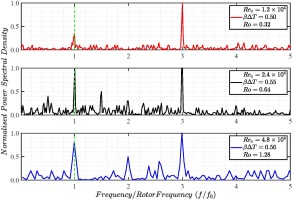
Figure 8.

Measured normalised power spectral density of the tangential velocity in the mid plane of cavity 3 at a radial location of r/b = 0.86 (Ω = 33.25 Hz).

The physical mechanism behind the formation of the power spectral density as shown in Figure 7 can be described as follows. If the measuring point of the tangential velocity is located towards the outer part of the circulation region, the tangential velocity signal records a value higher than that of the solid body rotation (Vθ>Ωr) when a cyclonic circulation (which by definition has the same sense of rotation as the disc) is encountered. The opposite is true (Vθ<Ωr) when an anticyclonic circulation is present at this radial location. During one full revolution of a single pair of cyclonic and anticyclonic vortices around the disc axis, there exists one peak and one trough in the tangential velocity temporal signal collected from a fixed circumferential location. A signal with approximately the same frequency as that of the solid body rotation is detected when a full rotation happens. The dominant frequency would therefore be doubled or tripled if two or three pairs of vortices exist. It is worth noting that although this explanation may imply that the size and the shape of the vortices would be identical, in reality they are different.

As shown in Figures 7 and 8, the spectral content of the tangential velocity changes with time. Figure 7 shows the recorded data at the beginning of the test at radial location r/b = 0.91 and Figure 8 shows the frequency signal at the radial location r/b = 0.86 measured 15 s later. As an example, the spectral analysis of case 2 at the higher radius shows the existence of at least three pairs of vortices at the beginning of the test. The analysis of the data collected 15 s later at the lower of the two radii (but not far away from each other) suggests that the number of vortex pairs is reduced to two. This proves the transient and evolutionary nature of the vortical structures within the cavity. Although not clearly discernible from the above figures, due to the chosen x-axis scale, there is a 1–2% slip associated with the core flow in relation to the solid body rotation.

Figure 9 shows the reduced static pressure contours obtained from the transient numerical study. Two different time instances, the first one after two disc revolutions and the second one after 30 disc revolutions are shown. The lows and highs of the reduced static pressure can be used to identify the regions of cyclonic and anticyclonic circulations respectively. The regions with anticyclonic circulations are annotated as A1, A2 and A3 whereas cyclonic circulation regions are denoted by C1, C2 and C3. The black solid circles represent the radial locations where the spectral analysis was conducted experimentally. The white dashed circles illustrate the bore region below the disc cob. As seen in the experimental data presented in Figures 7 and 8, the number of vortex pairs present in the numerical solutions reduce from 3, at the end of 2 revolutions to 2 after 30 revolutions.

Figure 9.

Computed time evolution of incompressible reduced static pressure (Pa) field with superimposed relative velocity (ms⁻¹) vectors (case 2):Ro=0.64, Rez=2.4×104, Reθ=7.1×105 and βΔT=0.55 at cavity mid plane (z/s = 0.5).

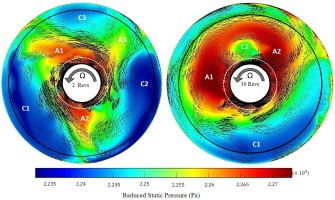
It is worth nothing that the labelling of the cyclonic and anticyclonic zones is only for illustration of the flow structures inside the cavity. It is not; however, clear if their numbering sequence is correct in that A1 may not necessarily be paired with C1 etc. The changes in the pairs of vortices present with time will be discussed later in this paper in the numerical results part.

Transient βΔT

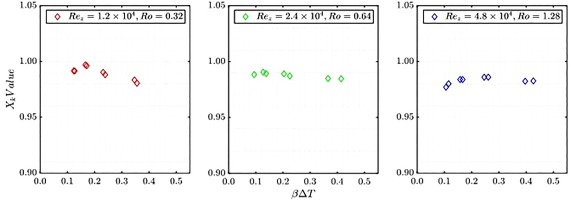
The flow visualisation and LDA measurements for rotating cavities with an axial throughflow with either the discs or the shroud heated showed that a secondary toroidal flow inside the cavity is generated by the axial jet of fluid. The strength of such a flow grows as the gap ratio (G) and the Rossby number (Ro) increase. For instance, the impact of the axial throughflow diminishes at the higher radial locations inside the cavity and consequently the buoyancy effects dominate when solid body rotation is present. At the lower radii, the effect of axial throughflow has been observed where the free vortex flow occurs and the strength of recirculation increases. Therefore, the heat transfer inside these cavities includes forced convection (generated by the axial flow) at lower radii and free convection (generated by the buoyancy dominated flow) at higher radii. Here, in this section, the flow structure inside the cavity is investigated differently by observing the sensitivity of rotational effects due to the variation in buoyancy parameter (βΔT) transiently. To enable this, the rig is heated up until the steady state mode is reached for a given throughflow. Steady state is thought to be achieved when the temperature variation sensed by the thermocouples anywhere in the cavity is less than 0.2 K over a duration of 5 min. Once steady state is reached the external heat source is turned off. The LDA data is then acquired at a number of quasi steady conditions as the rig cools down gradually and consequently as the value of βΔΤ decreases. The acquisition time of LDA recoding is similar to that of the steady cases and it is 15 s per measurement. The number of particles may vary in the different radial locations but it is nominally set to 5,000 samples. This helps to prevent significant and abrupt changes of the flow conditions in the transient measurements.

The LDA measurements are conducted for these transientβΔTconditions at the mid plane (z/s = 0.5) of cavity 3 starting with steady state condition defined by the cases 1 to 3 as described previously. The data is presented for two radial locations, r/b = 0.67 and 0.91 by plotting the variation of the swirl value defined as Xk=(Vθ/Ωr). Figure 10 shows the data for the lower of the two radial locations, r/b = 0.67. The swirl value is seen to decrease progressively, albeit to varying degree, for all three cases as βΔΤ increases. As discussed before, at the lower radii the effect of axial throughflow is relatively strong. It can be seen that the sensitivity of swirl (X_k) to the buoyancy parameter (βΔΤ) reduces as the axial Reynolds number increases. For the lowest Ro the swirl value drops by about 10% when βΔΤ increases from 0.1 to 0.4. However for the highest of the Ro tested the drop in X_k for a similar change in βΔΤ is only about 1%. Figure 11 shows a similar data but captured at the higher of the two radii, r/b = 0.91. The X_k value for all cases is nearly unity but it decreases only slightly when βΔΤ is increased compared to those observed at the lower radius for each case. This is consistent with the literature discussed above. This is therefore further proof that, unlike near the bore, axial throughflow does not play any role at the outer radius to change the swirl value.

Figure 10.

Measured transient variation of X_k value, at cavity 3 mid plane (z/s = 0.5) and the radial location of r/b = 0.67.

Figure 11.

Measured transient variation of X_k value, at cavity 3 mid plane (z/s = 0.5) and the radial location of r/b = 0.91.

Numerical results

The numerical analysis is performed for the condition specified by case-2 of the experimentation. This corresponds to; Ro=0.64,Reθ=7.1×105, Rez=2.4×104and βΔT=0.55. Plots presented in this section are at the mid-plane (z/s = 0.5) between discs 3 and 4 and located in the cavity 3. The results discussed here show the temporal evolution of flow for time-steps corresponding to 2, 17 and 32 revolutions of the rotor. The radial location of the cavity bore in the figures presented are shown by dashed black circles to aid the flow structure observations. The sense of the disc rotation is anticlockwise.

The reduced static pressure, P∗ is defined as:

This parameter can be assumed as equivalent to static pressure corrected for centrifugal pressure rise at each radial location. Owen et al. (1985) showed that the cyclonic and anticyclonic circulations are the regions where P∗ is low and high respectively. Farthing et al. (1992a) showed a schematic diagram of the flow in their model. The results shown here have promising similarities to the above model.

Figure 12 shows the computed reduced static pressure in the radial-circumferential (r−θ) plane of cavity 3. Three pairs of vortices are visible in Figure 12a that corresponds to a time-step after 2 disc revolutions. These are identified by the three low pressure regions with cyclonic circulation (C) that co-exist with the three high pressure cells with anticyclonic circulation (A). The pairs are circumferentially spaced by approximately 120 degrees intervals. The strength of each pair is different because the structures are not identical in size and shape. Figure 12b shows the pressure contours corresponding to a time-step in the 17th revolution. A single strong pair of vortices can be seen. A powerful anticyclonic cell interacts with a strong cyclonic circulation. For a time-step after 32 revolutions, Figure 12c shows a strong cyclonic circulation (C1) which is paired with a strong anticyclonic circulation located in the west of the cavity (A1). A pair of weak vortices that are paired together in the approximate north to north-east of the cavity (A2 and C2) are also seen in Figure 12c. These two vortex pairs are strongly visible and well established in Figure 12c. This shows that the number of pairs of vortices could change with time and that the flow structure inside the cavity is unstable and unsteady.

Figure 12.

Computed time-sequence of incompressible reduced static pressure (Pa).

Owen (2010) suggested the following relationship between the cavity radius ratio, a/b, and the number of pairs of vortices, N, where

The number of pairs of vortices (N) calculated in this manner for the present cavity test case where the radius ratio of the annulus a/b ≈ 0.32 is 3. As shown above, although there is a good agreement between this relationship and the numerical study, the suggested number could change further with time. This is also seen in the experimental data where the spectral analysis showed three pairs of vortices initially which then changed to two pairs of vortices. The results also show that the value of N is not only a function of a/b but there are other parameters such as the axial and rotational Reynolds numbers that should be considered. The unsteady and unstable nature of the flow structure within the cavity was also observed and stated by various researchers including (Tian et al., 2004; King et al., 2005; Atkins & Kanjirakkad, 2014).

The normalised density change (Δρ/ρ) and the temperature change (delta T) within the cavity with respect to the corresponding upstream inlet values in the r−θ plane of cavity 3 is shown in Figure 13. The normalised density change is defined as:

Figure 13.

Computed contour plots of instantaneous density change and cavity delta T (K) within cavity 3 mid plane (z/s = 0.5).

where ρlocal is the instantaneous density at the local point and ρinletis the density of the domain inlet upstream. Plotting this density variation (Figure 13a–c) gives a good indication of the radial migration of fluid in and out of the cavity including the formation of the radial arm. The temperature change within the cavity, delta T, is calculated as (Tlocal−Tinlet) and can be seen (Figure 13d–f) to correspond well with the density change plot. Both images show the time evolution of the flow structures through the 2nd, 17th and 32nd revolutions with the corresponding timestamps of 60, 510 and 960 ms respectively. The near zero value of the parameter Δρ/ρ in the bore region in Figure 13a suggests that the density of the cold bore flow is preserved from the upstream inlet to the mid axial plane of cavity 3. Cold bore flow is seen to migrate radially outward into the cavity along two branches that are located at 5 and 10 o’clock positions. Figure 13d, for the same revolution, shows that most of the cavity is filled with hot air (ΔT>80) as the two branches of the cold air form a radial arm as they enter to the cavity. Hot air from the shroud can be seen to migrate radially inward on either side of the radial arm in order to satisfy mass continuity within the cavity. Figure 13b and e show further development of the radial arm as it impinges on the shroud and bifurcates into two circulation zones; cyclonic region (rotating in the same direction of the cavity walls) and anticyclonic region (rotating in the opposite direction of the cavity walls). As the circulation zones are shaped, the circumferential pressure gradient produces the Coriolis forces necessary for the radial arm of the cold air to be formed (Farthing et al., 1992b). Figure 13c shows that the radial arm at 10 o’clock tends to travel circumferentially further after impinging on the shroud and meets with the cyclonic zone of another radial arm located at the 2 o’clock position. The quantity Δρ/ρ is at its local minimum at these two regions. The axial throughflow of cold air is seen to travel radially outward at 2 o’clock in Figure 13f to form the second radial arm. 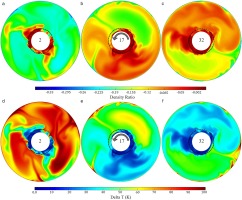This cycle is repeatable with time but the number of pairs of vortices is not predictable.

The experimental and numerical investigation into the unstable flow structure within a heated rotating cavity by Bohn et al. (2006) reported a repeatable flow pattern fluctuating between one, two, and three pairs of vortices in a periodic manner. The current results have shown this unstable nature, however, the periodicity of the changes could not yet be established from the 35 revolutions that were numerically simulated.

Time averaged data

The time averaged results from the numerical simulation, of which the instantaneous data was shown in the previous sections, is presented here. The data is averaged both temporally and spatially. The mid plane of cavity 3 includes 90 K numerical ‘measurement points’ consisting of 250 radial and 360 (one degree apart) circumferential points. The data averaging was started after the 20th revolution and was continued up to the 45th revolution. The number of time-steps made available to be averaged for each revolution is 360.

Figure 14 shows the data time averaged over 1, 10, 20 and 25 revolutions. The average axial (Vz) and radial (Vr) velocity components and the swirl value (Xk) are shown. The dashed black line represents the cob region. Axial flow velocity and bulk radial flow velocity within the core region is nearly zero for most of the cavity. This is consistent with existing knowledge. Near the cobs (where the cavity fluid interfaces with the bore flow), where the radial velocity is non-zero reflects on the radial inflow and outflow that manifest in this axial plane. The positive value of the radial velocity at the mouth of the cavity (dashed line) shows that there is a net radial outflow from the bore region into the cavity at this axial plane. The time invariant nature of the radial and axial velocity profiles suggest that the axial throughflow and the amount of the bulk radial flow in and out of the cavity is established very early on in time. The normalised circumferential velocity component (Xk=Vθ/Ωr) on the other hand has the highest freedom for temporal variation within the cavity as the radial arm and the associated vortical structures develop and evolve with time in terms of size shape and number.

Figure 14.

Computed axial (Vz) and radial (Vr) velocity components and the swirl value (Vθ/Ωr) from the cavity 3 mid plane (z/s = 0.5) averaged at the different times.

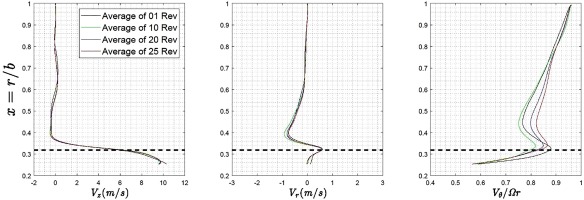
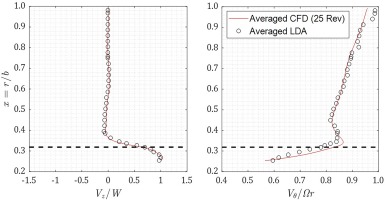
Figure 15 shows the comparison between the LDA experiment and the time averaged numerical data. The LDA data is inherently time averaged and there are 35 radial measuring points from the bore to the shroud. The CFD data shown is the time average over 25 revolutions. The normalised axial velocity (Vz/W) and the swirl value (Vθ/Ωr) are shown in this figure. The agreement in both distributions is encouraging. This is particularly so considering that the time over which data is averaged for the CFD is only worth 0.75 s (25 revolutions) compared to the 15 s over which LDA data is typically collected and averaged at each measurement point.

Figure 15.

Comparison between the LDA (measured) and time averaged CFD (computed) data.

Conclusions

The experimental and numerical results from the Multiple Cavity Rig (MCR) at the University of Sussex are presented. The experimental data consists of LDA measurements of the axial and tangential velocity components within a heated rotating cavity with axial throughflow. The data corresponds to three axial Reynolds numbers at a fixed value of rotational Reynolds number. The spectral analysis of tangential velocity component is performed for these conditions. The numerical data presented is from Unsteady Reynolds averaged Navier-Stokes simulations conducted at one of the experimental conditions that is presented. The major conclusions of this work are summarised below.

The spectral analysis of the circumferential velocity obtained from the LDA indicates the temporal and spatial evolutionary nature of the flow structure within the cavity. For each of the three Rossby number cases presented, frequency peaks were detected at twice and three times that of the solid body rotation suggesting the existence of two and three pairs of cyclonic and anticyclonic circulations respectively. Furthermore, similar measurements obtained after a short (15 s) time gap suggests a change in the number of frequency peaks and hence that of the vortex pairs present.

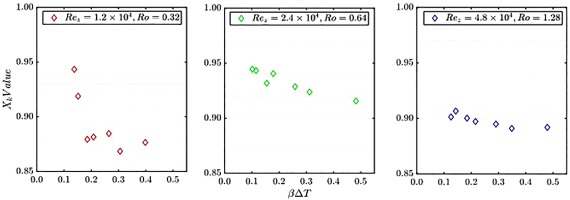
Measurement of the buoyancy parameter (βΔT) conducted transiently as the rig is cooled down in a quasi steady manner showed the sensitivity of the swirl value (X_k) at locations within the cavity. It has been shown that, at a radius just above the mid cavity height (r/b=0.67), this sensitivity is highly dependent on the Rossby number (Ro). At the lowest Rossby number tested (Ro=0.32), the swirl value reduces by about 10% as βΔT is increased from 0.1 to 0.5. At the highest Rossby number tested (Ro=1.28) this sensitivity diminishes substantially as the reduction in X_k is only 1% for a similar variation in βΔT. At a higher radial location closer to the shroud (r/b=0.91), however, where the flow is at near solid body rotation, there is very little sensitivity for X_k with βΔT. The behaviour at both these radii are consistent with the dominant effect of buoyancy near the shroud and of throughflow closer to the bore.

Instantaneous contours of computed reduced static pressure in the r−θ plane from unsteady numerical simulations for one of the three experimental cases (case-2) show evidence of the transient behaviour in the number of vortex pairs present at any one time. This, therefore, support the spectral analysis data from the experiments. The formation of the radial arm with the associated vortices and their evolution in time and space is further illustrated using contours of density and temperature differences in the cavity.

Time averaged radial distribution of computed axial and radial velocities show the early establishment of bulk motion along these directions as the profiles change very little with time. The time averaged radial distribution of the normalised circumferential velocity (X_k) however changes as the averaging window is changed. These are consistent with the understanding that axial and radial velocities are nearly zero in the core of the cavity whereas the circumferential component has much more freedom to change as the rotating structures evolve. The time averaged radial distribution of axial velocity and swirl over the longest time average period presented (25 revolution) compares very well with the inherently time averaged data from the LDA experiment.

Nomenclature

Abbreviations