Introduction

Conventional power plants must compensate fluctuations in the power supply because of an increasing amount of volatile renewable energy sources such as wind and solar power. This demands more flexible conventional power plants. Gas turbine power plants adjust total power output quickly but CO and UHC emissions limit the part load regime to about 60% of the full load. This study focuses on the operational range extension of gas turbines in a combined cycle power plant to lower loads. The basic idea to accomplish this goal is to increase the reactivity of the fuel and to reduce the possible overall equivalence ratio in the combustion chamber without risking increased emissions, flame out or combustion instabilities. The desired increase of reactivity is achieved by converting methane to hydrogen.

There are mainly three different approaches to convert methane to syngas with high hydrogen content: partial oxidation (POX), steam reforming and autothermal reforming 20.

POX is a combustion process in the very rich regime. Thermodynamic equilibrium is shifted towards carbon monoxide and hydrogen due to the deficiency of oxidizer. Usually a catalyst is used to increase the reactivity of the mixture. Regarding conversion to hydrogen and residence time the studies of 04 and 08 show that POX with an affordable nickel catalyst shows promising results. However, the produced syngas has a very high temperature, which impedes premixing due to auto-ignition, and thus a clean burn out in the combustion stage. Cooling the syngas to reach a temperature which allows for premixing can only be achieved with a significant pressure loss that incorporates a heat exchanger.

The second route to produce syngas is steam reforming 12. In steam reforming, natural gas is mixed with water vapour. Water and natural gas react mainly to carbon dioxide and hydrogen. Usually steam reforming is performed with a high excess of vapour to avoid coking of the nickel catalyst and to increase the hydrogen yield. The reaction is highly endothermic (ΔHRo = 206 kJ mol−1). An external heat supply decreases the efficiency dramatically. Thus, a steam reformer cannot be used as fuel processor in this context.

The third process to produce syngas is autothermal reforming. An autothermal reformer (ATR) can be seen as a combination of the two aforementioned processes 24. Natural gas is mixed with an oxidizer and water vapour and reacts on the surface of a catalyst. The exothermic oxidation reactions provide the necessary heat supply for the endothermic steam reforming reaction. By adjusting the ratios of oxidizer to carbon bound in methane (Air/C) and water to carbon (H₂O/C), it is possible to control the temperature of the process and the products. The ATR is analysed in this study, because the moderate syngas temperature (below 1,000 K) allows for premixing, no external heat supply is needed and the residence time for the conversion is reasonable.

Fuel reforming prior to combustion has been particularly in the focus of researchers because of its potential to CO₂ sequestration. The high partial pressure of CO₂ in the syngas provides the potential for membrane or chemical sequestration 13, 25. Several studies on fuel reforming for flame stabilization have been published in the past: Bozza et al. investigate the use of the enthalpy of the exhaust gas to reform the fuel 01. In CCPPs, this enthalpy flow generates steam for the steam turbine. Extraction of large amounts of exhaust gas enthalpy has a negative influence on overall plant efficiency. 19 discuss the possibility of exhaust gas recirculation, which has an equally negative effect on the Heat Recovery Steam Generator (HRSG) performance. A similar process is analysed by 07, but to enhance reactivity of biogas. All the aforementioned processes are designed for a stand-alone gas turbine process and cannot be implemented in CCPPs. Karim et al. deal with a catalytic rich quench lean process 09, 16, 22. A rich fuel air mixture is ignited catalytically. The reactor is cooled by bypassing air. For an effective cooling, the areas must be sufficiently large. This in turn increases the pressure loss. The authors do not mention how the pressure loss of the rich catalytic stage is thought to be compensated. In the present study, fuel reforming prior to combustion suitable for the integration in CCPP is analysed with respect to the general feasibility of the concept and the potential improvement of the turn-down ratio.

The paper is organized in the following manner. Firstly, the syngas generator is described in detail. In the main section, models for all components of the syngas generator and the gas turbine based on simple equations are presented. The components include an ejector, a catalyst bed, the syngas injection, the compressor, the combustion chamber, the turbine, and the HRSG. Thereafter the results of the model are discussed. Then a kinetic study shows the conversion of natural gas to syngas for the fuel processor. This is followed by the calculation of the laminar flame speed and the Damköhler number of mixtures of methane and syngas to assess the possible stability gain of the gas turbine in the part load regime.

Integration of the syngas generator for part load operation in a combined cycle power plants

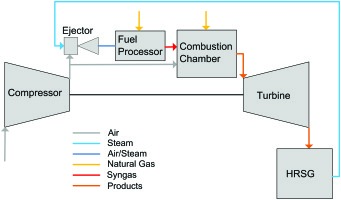
Figure 1 shows a CCPP process scheme with the catalytic reactor driven by an ejector. In full load operation of the gas turbine, the compressed air is entirely directed to the combustion chamber, where it is mixed and reacts with NG. The resulting hot gas drives the turbine, which itself drives the compressor and a generator (not shown). The ejector and the fuel processor are placed in a parallel flow configuration and are only used in the part load regime. In order to reduce power below full load the fuel mass flow is reduced as usual. This measure is limited by the lean blow out (LBO) limit of the fuel. Further power reduction is achieved by simultaneously throttling the compressor air intake and the fuel mass flow, at a constant combustion temperature. With state of the art compressors intake can be reduced to ~70% of the full load air mass flow. At this point, LBO limits the power reduction again. This is where the fuel processor is activated. Steam generated by the HRSG is used to boost a small fraction of the compressed air to higher pressure. This air is directed through the fuel processor. Natural gas is mixed with this air and water vapour flow. This mixture is then converted to syngas at the catalyst. Finally, the syngas is injected into the combustion chamber in parallel with the remaining natural gas. The syngas and natural gas mixture has a higher reactivity than natural gas alone and is thus suitable to combust at a lower equivalence ratio. The lower equivalence ratio results for a constant air mass flow in less fuel and thus the total power output can be reduced.

Figure 1.

Process scheme of gas turbine equipped with the autothermal on-board fuel processor.

The operation of a fuel reformer directly upstream of the combustor leads to some challenges regarding the system integration. One of the challenges is the pressure loss this bypass incorporates. The air exiting the compressor is split into two flows: one for the catalytic reactor, which produces syngas to be injected into the combustion chamber, and the second that is led directly into the burners of the combustor. For this reason the driving pressure for the syngas generator must be generated. In order to achieve reforming in a compact device a catalyst must be employed. Literature on syngas generation indicates that nickel catalysts are most favourable for reforming because nickel exhibits high activity at low catalyst cost. Problematic is the high light-off temperature of the nickel catalyst. Light-off temperature of nickel catalysts are at least 700 K 26. If the temperature of the mixture of compressed air, steam and natural gas is too low for a nickel catalyst to achieve ignition, a second catalyst with a lower light-off temperature must be employed. For the ignition, a platinum/palladium catalyst can be implemented. The operation of the catalytic fuel processor is accompanied by a significant pressure loss. By the integration of an ejector upstream of the reactor, this pressure loss can be compensated. The ejector is driven by the high-pressure steam extracted from the HRSG. In full load operation this steam has approximately a temperature of 800 K and a pressure of 120 bar 05. The catalysts perform well within a certain temperature range. Below this range the activity is lost — above it the catalyst is damaged. Therefore, syngas temperature is a crucial parameter for the design of the syngas generator.

In the following, a detailed model is introduced which allows to identify the limits of the operating range of the catalytic reactor as function of the mass flow of steam and air related to the natural gas flow at inlet of the reactor, as these two ratios are the only free design parameters.

Model of the syngas generator integrated in the gas turbine cycle

The compressor, the ejector, the catalyst bed, the combustion chamber, the turbine, and the HRSG are modelled focussing on the necessary information to evaluate the feasibility of the syngas generator concept. The model is based mostly on analytic equations. For some parameters, e.g. the adiabatic efficiency of the compressor or the steam data, look-up tables are used. Details of the modelling for each component are given below. After the description of the components, the solution algorithm and the results are discussed. The model can also be used to investigate the sensitivity of the process to certain input variables. For this reason, a sensitivity analysis is additionally presented.

Syngas generator

The syngas generator comprises the ejector and the catalyst bed.

Ejector pump

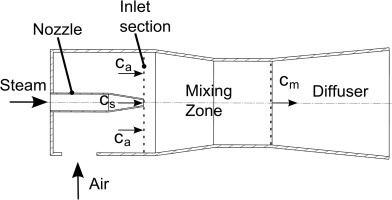
An ejector pump comprises a nozzle for the driving fluid, an inlet for the driven fluid, a mixing zone, and a diffuser (see Figure 2). Details on the operation and performance of ejector pumps can be found in 27. In the present case, a Laval nozzle is used to attain supersonic conditions. In the nozzle, kinetic energy of the steam is generated with very high efficiency. The driving jet exits the nozzle and entrains the air. The mixing process is nearly isobaric, but involves some friction losses. In the diffuser downstream of the mixing zone the kinetic energy is reduced continuously associated with a pressure gain. The mixture pressure at the exit of the ejector pump is between the pressures of the driven and the driving fluid.

Figure 2.

Scheme of an ejector pump.

For the isobaric mixing zone 17 the momentum balance reads as follows:

(1)

 cm=m˙scs+m˙acam˙s+m˙a−Ffrm˙s+m˙a

is solved for the mixture velocity c_m as a function of steam and air velocities (c_s, c_a), mass flows (m˙s, m˙a) and friction F_fr. The friction losses are relatively small and are assumed to be of the order of: Ffrm˙s+m˙a = ζ12dmCm = O(0.01)Cm. The velocities in the momentum balance are replaced via an energy balance () by enthalpy differences and the according efficiency of the energy conversion:

(2)

 ci=2Δhiηi

Introducing these equations in the momentum balance and solving for the mass flow ratio of interest, i.e. steam to air, gives:

(3)

 m˙sm˙a=(1+ζ12dm)−ΔhaΔhcompηinηdifΔhexpΔhcompηNηdif−(1+ζ12dm)

Here the ΔhexpηN is the enthalpy difference of the driving fluid, which is converted to kinetic energy in the nozzle, Δhaηin is the corresponding enthalpy difference for the air converted in the inlet, and Δhcomp is the enthalpy difference the mixture has to undergo to achieve the necessary pressure level. The efficiencies and the friction coefficient are calibrated to meet experimental data presented in 17. Resulting values are shown in the .

The unknown enthalpy differences are treated as follows. The enthalpy difference Δha takes different values for each operating point. The enthalpy difference and inlet velocity depend on each other. An inlet cross section is defined to give the optimal inlet velocity and thus the optimal enthalpy difference for a reformed natural gas mass flow of 50%. As the inlet air velocity c_a is rather small, the change of state can be regarded incompressible. Thus, the definition of an inlet cross-section for a certain operating condition specifies the air inlet velocity and the corresponding enthalpy difference for other operating conditions as well. Two states of the steam are relevant for the definition of Δhexp. Firstly the state of the steam provided by the HRSG and secondly the state at the inlet plane of the mixing cross-section. The former depends on the load of the gas turbine and is described in detail below. For the latter, it is assumed that the nozzle is designed in such a way that for 50%-reformed-fuel-operation the steam pressure in the exit plane of the nozzle reaches exactly the same pressure as that of the air prior to mixing. The Δhcomp accounts for the difference in enthalpy in the diffuser. At the exit plane of the mixing zone, the gases are assumed to be perfectly mixed. The kinetic energy of this mixture is converted to static pressure in the diffuser. The mixed state is defined by adiabatic, isobaric mixing. The pressure at the end of the diffuser must match the sum of the compressor outlet pressure and the pressure loss induced by the catalytic reactor and the fuel injector.

Catalyst bed

For the catalyst bed, the temperature of the products and the pressure loss are of importance. The temperature of the products must be within a certain range to avoid overheating and damaging of the catalyst and to maintain reactivity. This range is assumed to be 900K = T_min < T_syngas < T_max = 1,123 K based on data from literature. The thermodynamic equilibrium based on minimization of the free Gibbs energy is calculated for the mixture of methane, air, and water vapour in the reformer. The species involved in these calculations are CH₄, CO₂, CO, solid carbon, H₂O, H₂, O_2, and N₂.

The pressure loss of a catalyst consisting of pellets can be calculated according to the Ergun equation 06:

(4)

 ΔpΔL=A(1−Ψ)2Ψ3ηcd¯p2+B(1−Ψ)Ψ3ρc2d¯p

For the employed nickel catalyst the Sauter diameter d¯p is assumed to be 6.8 mm. This value corresponds to commercial 10-hole ring catalysts that are typically used in reforming.

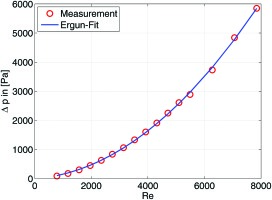
The coefficients A and B in are fitted to pressure loss measurements with cold-air performed on a generic tube reformer filled with commercial 10-hole rings. The Reynold’s number Re is defined with the cold-air properties, the superficial velocity, and the Sauter diameter as characteristic length scale. The measurements and the corresponding fit are presented in Figure 3. For the reacting case, the fluid parameters such as density and viscosity change over the length of the reactor. In this case, the reactor is discretized into ten segments and the fluid parameters are adjusted to the change in composition and temperature. It is further assumed that in the reformer the aforementioned equilibrium is reached at the outlet and that the composition changes according to an exponential decay towards the equilibrium composition. This corresponds well to the simulated change in composition that is described later in this study. The residence time is assumed 0.2 s. The size of such a reactor is given in .

Figure 3.

Pressure loss of the catalyst bed.

Results of the process model

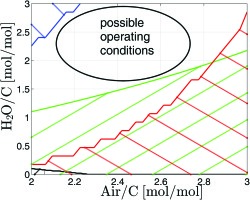
The four major constraints governing the operational window are illustrated in Figure 4. The operational window covers a stripe from Air/C ≃ 2.0 and H₂O/C ≃ 1.75 to Air/C ≃ 2.75 and H₂O/C ≃ 3. If the amount of air is increased too far, overheating occurs (red hatched area). By increasing the amount of water, deactivation becomes a problem (blue hatched area). Carbon formation seems to be of minor importance as the black area indicates. Only for mixtures with no or little water solid carbon is formed. In the black hatched area in Figure 4 the equilibrium carbon share is greater than 1 ppm. The green hatched area cannot be reached, because the ejector cannot generate the pressure gain required for operating the syngas generator. With an increasing amount of air, the load for the ejector also increases, as does the total mass flow through the syngas generator. Thus, the driving pressure rises and the ejector needs more water vapour to pump the air. Above a ratio of H₂O/C ≃ 2.2 the pressure gain in the ejector is sufficient for all air mass flows considered.

Figure 4.

Operating Window: Blue: Low temperature deactivation; Red: High temperature deactivation; Black: Carbon formation; Green: Pressure constraint.

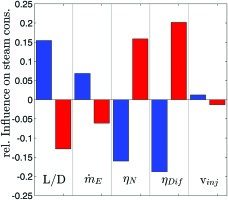
In addition, a sensitivity analysis has been performed. Several design parameters of the syngas generator affect either the pressure loss or the pressure gain in the ejector. Figure 5 shows the five most significant parameters governing steam consumption. Increased steam consumption moves the pressure boundary in Figure 4 (green) upwards and thus reduces the operational window. Due to the correlation of the effective velocity caused by the length-to-diameter ratio of the catalytic reactor L/D, it has a major influence on the pressure loss of the reformer. The mass flow of fuel to be reformed and the injection velocity of the syngas have significantly weaker effects. Increasing the fuel mass flow by 10% increases steam consumption by only 5%. The most influential parameters are the ejector nozzle and diffuser efficiencies. The most important outcome of the sensitivity study is the finding that proper ejector design is crucial to obtain the highest possible efficiencies and a wide operability range.

Figure 5.

Sensitivity analysis: L/D: Length-to-width of the catalytic reactor; m_E: Mass flow of fuel to be reformed; η_N : Nozzle efficiency; η_Dif : Diffuser efficiency; c_inj : Velocity of the syngas injection; Blue: 10% positive change; Red 10% negative change of the independent variable.

Kinetic study of the catalytic reactor

With the model of the catalytic reactor based on detailed chemistry the efficiency of syngas generation is calculated. Achieving a high hydrogen concentration in the produced syngas is essential because it governs the syngas reactivity. An important optimisation criterion is the minimisation of the residence time because it influences the size of the catalytic reactor and its pressure loss.

Results of the kinetic study

For the reactor analysis in the current context, Air/C = 2.5 mol·mol^-1 and H₂O/C = 2.5 mol·mol^-1 has been selected, which represents an operating point inside the operating window identified above. The other settings such as size of the fuel reformer, mass flow to be reformed and so forth are the same as those modelled before, see . A heat loss of 10% of the converted higher heating value is introduced to account for the heat losses of the syngas generator. This value fits best to measurements on a syngas generator test rig, which will be published subsequently. The results of the calculation at 20 bar are depicted in Figure 6 and in Figure 7.

Figure 7.

Calculated gas temperature: 0–20 ms noble metal catalyst for ignition, 20–225 ms reforming catalyst.

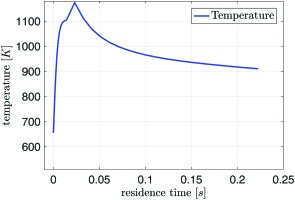
Figure 6.

Calculated species mole fractions: 0–20 ms noble catalyst for ignition, 20–225 ms reforming catalyst.

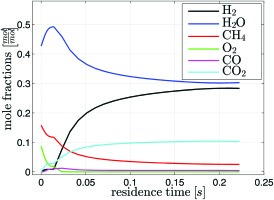
In the investigated case, combustible gas has a residence time of 20 ms in the ignition catalyst. After ignition, oxygen and methane are consumed while water and carbon dioxide are produced. Only very little hydrogen and carbon monoxide are created. A significant temperature rise from 650 K to 1,100 K is calculated. Reforming occurs in the second catalyst stage. Here mainly water and methane are consumed to produce hydrogen and carbon dioxide. The vast amount of water in the mixture suppresses the production of carbon monoxide via the shift reaction. As the reactions in the reforming stage are endothermic the temperature drops to 910 K The sudden increase in temperature at the entrance of the second stage does not happen in reality. Apparently, the reaction mechanism is not designed to cope with oxygen in the reactants. The activity is overestimated. However the calculated methane conversion of 80% within the given residence time is in line with data from literature 15. The final composition of the mixture is approx. 30%-vol water, 30%-vol hydrogen, 30%-vol nitrogen, 10%-vol carbon dioxide, and a few percent of methane. The syngas contains hardly any oxygen or carbon monoxide. For other ratios of water and air to fuel inside the operating window, the general trends for the syngas composition and temperature are similar.

Calculation of the laminar burning velocity

The one-dimensional laminar burning velocity of the syngas and methane mixture has been calculated to evaluate the effect of syngas addition on combustion stability. The calculation was performed with the GRI3.0 mechanism 23, which has been designed for methane. Since it incorporates hydrogen and carbon monoxide mechanisms, it can also be applied to syngas and syngas/methane mixtures. In the subsequently presented cases, the air temperature is 673 K, the methane is assumed to have a temperature of 300 K, and the syngas temperature is 910 K, according to the results of the kinetic model presented in the last section. The total pressure is held constant at 20 bar.

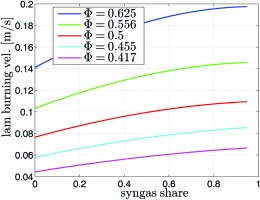
Two different sets of calculations were performed. In the first case the laminar burning velocities for mixtures with an increasing share of syngas at constant equivalence ratio was calculated. The syngas share corresponds to the amount of natural gas that is reformed. A non-stretched free flame was implemented to first calculate the methane flame with different equivalence ratios. Then the share of syngas in the fuel was increased at constant equivalence ratio and the laminar burning velocity of the mixture was determined. The results of this calculation are shown in Figure 8. With an increasing syngas share, the laminar burning velocities are increasing. For the ϕ = 0.5-case pure methane has a laminar burning velocity of 7.6 cm·s^-1, which is increased by a substitution with 50% syngas to 10 cm·s^-1, an increase of 32%.

Figure 8.

Unstretched one-dimensional laminar burning velocity of syngas and methane mixtures calculated with the GRI3.0 mechanism 23.

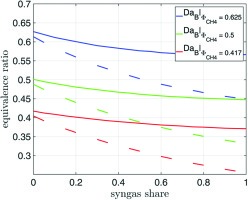
In the second case, the goal of the computations was to find the equivalence ratio of syngas/methane mixtures, which exhibits the same Damköhler number Da_B as that of methane. Correlations for the LBO equivalence ratio based on a Damköhler number, defined as DaB=τresτchem=dUbsl2α=dUbslll are a common approach 21. 28 apply such a correlation to LBO data for a swirl combustor with varying CO, H₂ and CH₄ content as fuel. The correlation fits well to the data for low H₂ content in the fuel. To obtain a better fit for low and high H₂ content data the authors introduce a term which accounts for the preferential diffusion effect of H₂. They argue that due to this diffusion effect the local equivalence ratio changes. This change is termed Δϕ =  ClnDFDO. Zhang et al. propose a value of 0.1 for the constant C. This value is adopted. The diffusivities of the fuel and oxidizer are calculated as in 28. The characteristic length scale d is assumed constant. The velocity of the burned mixture Ub=UoTbT0 scales with the ratio of the adiabatic flame temperature of the syngas and methane mixture compared to the pure methane case.

As can be seen in Figure 9, the equivalence ratio at constant Da_B is reduced significantly with rising syngas concentration in the fuel. The dashed lines correspond to the equivalence ratio corrected with the term for the preferential diffusion effect. Comparing the pure methane ϕ = 0.5-case with an injection of 100% syngas, the same Da_B is reached with a corrected equivalence ratio of ϕ = 0.33. According to the considered generic gas turbine, the total natural gas mass flow for part load is 11.9 kg/s, assuming a reduced air intake to 70% of full load intake and an equivalence ratio ϕ_CH4 = 0.5. On the other hand, the total natural gas mass flow that exhibits after conversion to syngas the same Damköhler number is only 9.4 kg/s. This corresponds to a decrease in thermal power of 20%. The detailed derivation is shown in .

Figure 9.

Solid lines: Equivalence ratio of syngas and methane mixture with the same Damköhler number as pure methane. Dashed lines: Equivalence ratio of syngas and methane mixture with the same Damköhler number as pure methane corrected with offset for the preferential diffusion effect.

Conclusion

The goal of the presented study was the analysis of the feasibility of an autothermal on-board syngas generator for improvement of the turn-down ratio of gas turbine combustors in unstaged operation.

Modelling reveals that an ejector pump driven by the steam produced in the HRSG can overcome the pressure loss induced by the catalytic reactor and the subsequent syngas injector in the burner. The temperature of the catalyst bed can be controlled by adjusting the Air/C and the Water/C ratios. An increasing amount of water reduces the temperature while more air results in rising temperature. Overheating and deactivation of the catalyst can be avoided by adjusting the mixture entering the catalyst bed. Carbon formation has been identified to be of minor threat for the catalyst. The analytic model shows that a wide operating window for the syngas generator exists.

Employing a sensitivity analysis, the length-to-width ratio of the fuel processor, the efficiency of the ejector nozzle, and the efficiency of the ejector diffuser have been identified as important design parameters. These parameters have a great influence on the pressure loss of the catalyst or the pressure rise in the ejector, respectively.

PFR type calculation with detailed chemistry reveal the general behaviour of the fuel processor. The resulting syngas has a hydrogen volume fraction of 30% and a temperature of 910 K. Calculations of the laminar burning velocity show a significant increase when substituting methane by syngas. This is also reflected by the calculation of the equivalence ratio for constant Damköhler numbers. A decrease of up to 20% of thermal power seems to be possible by reforming the fuel without increase of flame length or sudden blow-out.

The present study shows the feasibility of ATR for on-board syngas generation. The higher reactivity of syngas allows to improve the turn down ratio of gas turbine combustors in unstaged operation. Experimental data are only used to quantify the constants in and the heat loss in the kinetic model. As further steps, the conversion predicted by the kinetic model employed in the present study will be validated by experiments with a lab scale syngas generator, and the predictions of the operation range extension will be verified using the combination of the syngas generator and a premix burner equipped with injectors for syngas/methane mixtures.

NOMENCLATURE