Introduction

Lean premixed combustion is widely utilized to minimize the emission of NOx by reducing the peak temperature within combustor, while simultaneously maintaining low levels of other pollutants (Correa, 1998; Lewis et al., 1999; Lefebvre and Ballal, 2010). However, the combustion process in lean premixed systems is highly sensitive to noise disturbances, which can lead to undesirable thermoacoustic instability (Poinsot, 2017). Thermoacoustic instability is a challenging problem in many combustion systems especially in gas turbine combustors, which can result in high-amplitude pressure oscillations leading to loud noise, reduced efficiency, and even risks of structural damage. This instability arises from the coupling between acoustic waves and heat release fluctuations within the system, causing pressure oscillations that can grow in amplitude and cause combustor instability. Passive control methods have been proposed as a promising means to mitigate thermoacoustic instability without requiring major modifications to combustion system hardware. One of such technologies is the Helmholtz resonator, which works by absorbing acoustic energy, thereby disrupting the coupling between acoustic waves and pressure fluctuations in the combustor.

When analyzing the performance of a Helmholtz resonator in suppressing thermoacoustic instability, an isolated description of damper behavior is insufficient and requires investigation of the coupled system between the resonator and combustor. In modern gas turbine combustors, the temperature of combustion products can reach over 2,000 K (Palies et al., 2011). This hot gas flowing through the combustor duct is known as grazing flow. To protect the HR structure from erosion by the hot gas, a cooling flow, referred to as bias flow, is often introduced from later several stages of the compressor through the HR back cavity, and then passing through the HR neck. The temperature of this bias flow is typically between 500–800 K, with low Mach numbers (generally not exceeding 0.3) (Royce, 2015). Usually, the cross-sectional area of the HR neck is much smaller than that of the combustor, leading to a much smaller ratio of the mean mass flow rate of bias flow to grazing flow, therefore the mean flow parameters of the grazing flow in the combustor is generally considered to change slightly up- and downstream the HR. For this reason, this temperature difference is often disregarded during modeling. However, it is important to note that the mass flux oscillation of bias flow may be of the same order of magnitude as that of the grazing flow near the resonant frequency. When the cooling bias flow mixes with the hot grazing flow within the combustor, temperature disturbances are produced, thereby generating significant entropy disturbances. This has been demonstrated to be crucial in predicting thermoacoustic oscillations, but only has received little attention (Li and Morgans, 2015; Yang and Morgans, 2017).

In certain circumstances, increasing suitably the bias flow is necessary to withstand the periodic invasion of hot grazing flow into the neck region (Bellucci et al., 2004; Ćosić et al., 2015; Bourquard and Noiray, 2019; Miniero et al., 2023). When the ratio between the mass flux of the bias flow and the grazing flow (also dependent on temperature and other parameters) reaches a non-negligible value, the difference up- and downstream the HR inside the combustor duct in mean flow parameters becomes significant and cannot be ignored. This will be studied in the present paper. This paper is organized in the following way. Firstly, a new acoustic analogy model is derived, considering the two temperature difference effects mentioned earlier. This model combines the principles of mass, momentum, and energy conservation with a linear Helmholtz resonator model. The numerical method and simulation strategy are then explained. Mesh independence tests and verification against experimental results were conducted. In the Results and Discussion section, a comparison is made between the derived theoretical model and three existing models, followed by further comparison with the numerical results. The impacts of the temperature difference are discussed. Finally, the Conclusion section summarizes the key findings of the study.

Theoretical model

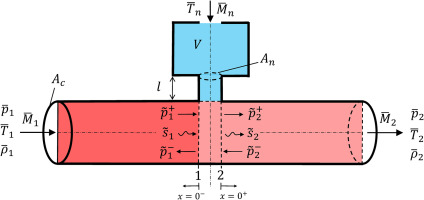
Figure 1 illustrates a one-dimensional combustion chamber equipped with a Helmholtz resonator (HR) on its side wall. The schematic shows various parameters such as the HR neck length (l), the combustor duct cross-section area (Ac), the HR neck cross-section area (An), pressure (p), temperature (T), entropy wave (s) and Mach number (M=u/c), with c the speed of sound and u the fluid velocity. Overscripts [p]¯ and [p]~ denote the mean and oscillation parts of the fluid parameters, respectively. Subscripts [p]1, [p]2 and [p]n denote the fluid parameters just before, after the HR and at the HR neck, correspondingly. Moreover, a mean flow having a low Mach number M¯HR≪1 and temperature T¯HR distinct from that present inside the combustor flows passes through the HR neck from the back cavity into the combustor. We assume that the cooling flow dominates the neck region, and thus, there is no occurrence of hot grazing flow intrusion, i.e. THR=Tn. In this study, we make certain assumptions, including (i) considering fluids in the system as single-component ideal gases using the gas law p=RgasρT, (ii) neglecting body forces, any heat addition and thermal diffusion, (iii) ignoring viscosity in the main body of the fluid except for near the HR neck region, where its effect is considered by using a HR model, (iv) assuming small perturbation amplitudes resulting in a linear system, (v) considering only plane waves in the combustor duct due to the low frequency (due to the low frequency of combustion instabilities, typically below 1 kHz, the dominant mode is often the plane wave mode) (Lieuwen and Yang, 2005).

Figure 1.

The Helmholtz resonator with cooling flow installed in a combustor duct.

https://journal.gpps.global/f/fulltexts/188265/JGPPS-00218-2023-01.01_min.jpg

Governing equation

The conservation of mass, momentum and energy for this one-dimension combustion duct gives

(1\rm a)
Ac(∂ρ∂t+∂(ρu)∂x)=δ(xh)m˙,
(1\rm b)
Ac(∂(ρu)∂t+∂(u2ρ+p)∂x)=δ(xh)f˙,
(1\rm c)
Ac(∂[ρ(CpT+0.5u2)]∂t+∂[ρu(CpT+0.5u2)]∂x)=δ(xh)e˙,
where Cp is the heat capacity at constant pressure which is in general a function of temperature, ρ the fluid density, δ(x) the Dirac delta function, m˙ the mass flux source term coming from the HR, f˙ the momentum flux source term coming from the HR (assuming that the neck flux is radially inwards with the combustor, so the momentum in the x-direction inside the combustor is constant, i.e., f˙=0) and e˙ the energy flux source term coming from the HR. The installation position of the HR is represented by xh, here xh=0.

Integrating Equation. (1) from sections 1–2 yields the mean flow conservation equations. Then by giving mean flow parameters upstream the resonator, ρ¯1, u¯1 and T¯1, and combining perfect gas relation, the mean flow parameters downstream the HR, ρ¯2, u¯2, p¯2 and T¯2, can be obtained. To obtain the acoustic governing equation, we linearize Equations. (1a) and (1b), subtract their respective mean quantity equations and keep only the first-order perturbation terms (due to the linear system), resulting in

(2)
∂ρ′∂t+ρ′∂u¯∂x+ρ¯∂u′∂x+u′∂ρ¯∂x+u¯∂ρ′∂x=δ(xh)m˙′Ac,
(3)
u¯∂ρ′∂t+ρ¯∂u′∂t+∂∂x(u¯2ρ′)+2∂∂x(u′u¯ρ¯)+∂p′∂x=0.

Due to the dynamic mixing of cold and hot flows, the system will naturally generate entropy waves. Therefore, the density perturbation will include the effect of entropy perturbations ρ′=p′/c¯2−s′ρ¯/Cp. By taking the derivative of Equation (2) with respect to time t, subtracting the derivative of Equation (3) with respect to space x, we can obtain

(4)
∂2ρ′∂t2−∂2∂x2(u¯2ρ′)−∂2∂x2(2u¯ρ¯u′)−∂2p′∂x2=δ(xh)Ac∂m˙′∂t.

This is our one-dimensional acoustic wave governing equation.

In order to obtain the relation between the up- and downstream pressure disturbances, Equation (4) needs to be solved. Equation (4) degenerates to a homogeneous equation in the regions up- and downstream of the HR (in x<0 and x>0 respectively), where the general solutions can be written as

(5)
p~1=p~1+e−ik1+x+p~1−eik1−x,p~2=p~2+e−ik2+x+p~2−eik2−x,

where [p]~ denotes the Fourier amplitude, k+ and k− denote the wavenumber

(6)
k1,2+=ωc¯1,2+u¯1,2,k1,2−=ωc¯1,2−u¯1,2,

By integrating once and twice of Equation (4) with respect to x across the source region, substituting the wave number Equation (6) and the expression for density disturbance ρ′=p′/c¯2−s′ρ¯/Cp, we can obtain

(7)
(1+M¯2)2c¯2+u¯2p~2+−(1−M¯2)2c¯2−u¯2p~2−−(1+M¯1)2c¯2+u¯2p~1++(1−M¯1)2c¯2−u¯2p~1−=ρ2¯u¯2Cp2s~2+m~nAc,
(8)
(1+M¯2)2p~2++(1−M¯2)2p~2−−(1+M¯1)2p~1+−(1−M¯1)2p~1−=ρ2¯u¯22Cp2s~2.

We note that integrating m~(x)δ(xh) over x gives the mass flux perturbation from the HR, i.e., m~n, which can be related to the pressure perturbation at the neck outlet, p~1, through a linear HR model based on the Rayleigh conductivity (Howe, 1979)

(9)
m~n=p~1F,

where F=−1/(c¯v2/(iωV)+iω/KRt), V denote the the HR cavity volume, c¯v sound speed in the HR cavity, ω the angular frequency, KRt the revised Rayleigh conductivity defined in references (Eldredge and Dowling, 2003; Rupp et al., 2010; Scarpato et al., 2012). Entropy perturbation s~ is unknown and can be obtained by combining m~n with the mass and energy equations. We derive the expression for s~ in the next section.

Entropy model

In order to obtain the oscillating entropy s~2, we linearise Equations. (1a) and (1c) and take the Fourier transform to give

(10)
m~1+m~n=m~2,(m¯2+m~2)(E¯2+E~2)=(m¯1+m~1)(E¯1+E~1)+(m¯n+m~n)(E¯n+E~n).

where E¯=CpT¯+(1/2)u¯2 denotes the mean stagnation enthalpy, with E~ the stagnation enthalpy perturbation. By combining Equation (10), the thermodynamic relation T~=(s~+Rp~/p¯)T¯/Cp and neglecting the second and higher order perturbations and assuming that the entropy perturbation upstream the HR inside the combustor is zero (s~1=0), we get

(11)
S~2=1T¯2m¯2{m~1ΔE¯12+m~nΔE¯n2+Ac(u¯1p~1−u¯2p~2)+(m¯1u¯1u~1−m¯2u¯2u~2)+m¯nE~n},

where ΔE¯12=E¯1−E¯2,ΔE¯n2=E¯n−E¯2. In this case, small terms of orders higher than or equal to O(M¯1) (e.g., u¯1ρ~1/(ρ¯1u~1)∼O(M¯1)≪1) can be neglected, due to the low mean flow Mach number in the combustor. Then, the expression of entropy perturbation comes to

(12)
S~2≈M¯1≪11T¯2m¯2{m~1ΔE¯12+m~nΔE¯n2}≈1T¯2m¯2{Acρ¯1u~1ΔE¯12+m~nΔE¯n2},

This expression demonstrates that the perturbation of entropy observed in the downstream section of the combustor depends on two factors, namely the variance in the mean stagnation enthalpy between the up-and downstream sections of the combustor as well as between the HR and downstream section of the combustor.

We have formulated a set of six equations, namely Equations (5), (7)–(9) and (11) with eight unknown perturbation parameters denoted by p~1, p~2, p~1+, p~1−, p~2+, p~2−, m~n and s~2. Combining Equations (5), (7)–(9) and (11) and reorganizing them into a matrix form, we have

(13)
[(1+M¯2)2c¯2+u¯2−(1−M¯2)2c¯2−u¯2−ρ¯2u¯2Cp2(1+M¯2)2(1−M¯2)2−ρ¯2u¯22Cp2Acu¯2(1+M¯2)Acu¯2(1−M¯2)T¯2m¯2]⏞B1[p~2+p~2−s~2]=[(1−M¯1)2c¯1−u¯1+FAc−(1−M¯1)2c¯1−u¯1+FAc(1+M~1)2(1−M~1)2Acu¯1(1+M¯1)+Acc¯1ΔE¯12+F(ΔE¯n2+u¯n2+Anu¯n)Acu¯1(1−M¯1)−Acc¯1ΔE¯12+F(ΔE¯n2+u¯n2+Anu¯n)]⏞B2[p~1+p~1−],

To ensure that the system is well-defined, two boundary conditions must be imposed. Typically, the boundary condition for the inlet and outlet are fixed. If p~1+ and p~1− are given, we can then obtain the solution when there is a discontinuity in the mean flow parameters inside the combustor up- and downstream the HR

(14)
[p~2+p~2−s~2]=B1−1B2[p~1+p~1−].

We designate the solution of the acoustic analogy model considering mean flow discontinuity between the up- and downstream of the combustor as MAA. In the subsequent section, we will consider a test case with given boundary condition, and use the Linearized Navier-stokes (LNS) solver in COMSOL to validate the results.

Numerical simulation

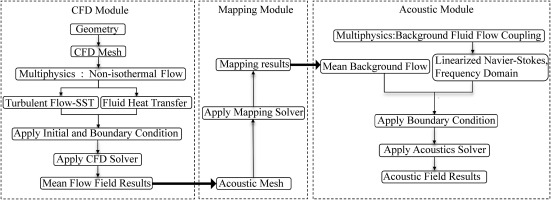
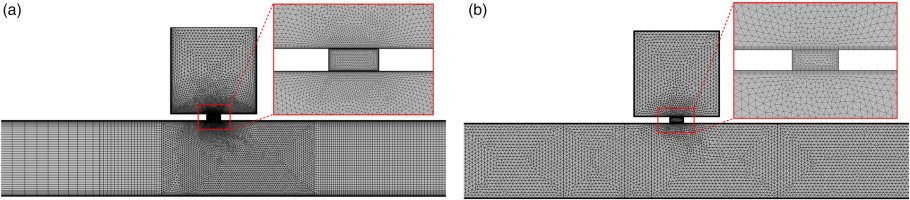
To validate the theoretical model, numerical simulations were employed, considering non-steady, compressible, and non-isentropic characteristics to accurately depict information from a three-dimensional flow field. This can be achieved by creating a 3D model of a Helmholtz resonator and combustor duct using COMSOL Multiphysics. The mean flow field results obtained from Computational Fluid Dynamics (CFD) are utilized as the background mean flow. The type of CFD simulation employed in this study is the Reynolds-Averaged Navier-Stokes (RANS) model. These results are inserted into the acoustic mesh using a dedicated mapping module to solve the linearized Navier-Stokes (LNS) equations in the frequency domain. The LNS and CFD governing equations employed in this study are consistent with those described in references (Lu et al., 2019; Wu and Guan, 2021; Dastourani and Bahman-Jahromi, 2021; Zheng et al., 2023). The solution methodology employed in the present simulation adheres to a flowchart, depicted in Figure 2.

Figure 2.

The processes involved in the numerical model of COMSOL.

https://journal.gpps.global/f/fulltexts/188265/JGPPS-00218-2023-01.02_min.jpg

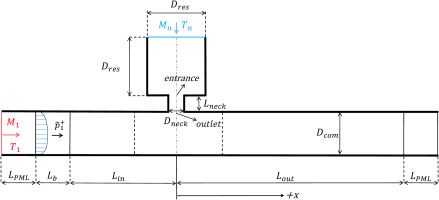
Table 1 presents the relevant fluid parameters utilized in both theoretical analysis and numerical simulations, as well as the geometric dimensions of the HR and combustor duct. Figure 3 shows a schematic view of the 3D model, LPML represents the length of the perfect match layer used at both ends of the duct, Lb is the length of the background sound field area, Lin and Lout the length of flow field upstream and downstream the HR respectively, Dcom the diameter of the combustor duct, Dneck the neck diameter of HR, Lneck the neck length, Dres both the diameter and height of the HR cavity. The boundary conditions applied for CFD calculations include a fully developed flow at the inlet and a pressure outlet. Additionally, a no-slip condition is imposed on the walls. On the other hand, for the acoustic calculations, the boundary conditions are as follows: the mechanical condition is set as slip, and the thermal condition is set as adiabatic. At the inlet and outlet, the perfectly matched layer (PML) boundary domain is used. The PML acts as a non-reflecting boundary condition, minimizing reflections of acoustic waves. Similar boundary conditions are detailed in (Dastourani and Bahman-Jahromi, 2021).

Table 1.

The geometries and flow conditions of the coupled HR-combustor model.

ParametersValuesParametersValues
Lneck/cm0.5V/m32.5×10−4
LPML/cm10An/m21×10−4
Lb/cm10T¯n/K500
Lin/cm60T¯1/K1,000
Lout/cm100p¯1/MPa2
Dcom/cm6M¯10.03
Dres/cm100M¯n0.03→0.06→0.09
Figure 3.

The schematic view of 3D coupled model in COMSOL.

https://journal.gpps.global/f/fulltexts/188265/JGPPS-00218-2023-01.03_min.jpg

Mesh independence and verification test

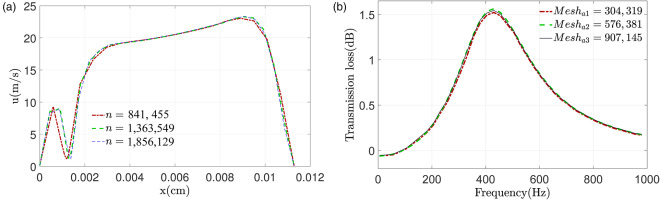
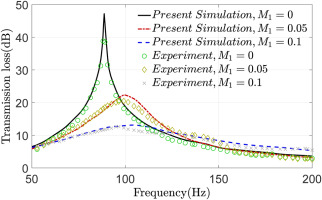
In order to validate the accuracy of the modeling approach, the geometric parameters of the model were adjusted to match those used in the experimental (Selamet et al., 2011). The simulated transmission loss results were then compared with the experimental results, as illustrated in Figure 4. To validate the mesh independence of the results in the flow simulations, three meshes with different number of elements were employed, with a total of Meshc1=841,455, Meshc2=1,363,549 and Meshc3=1,856,129 elements respectively. The investigation of mesh independence revealed that the computational results from the latter two meshes of CFD (the three meshes of Acoustics) exhibited convergence and were generally consistent, as shown in Figure 5. Two different meshes, comprising Meshc2=1,363,549 and Mesha2=576,381 elements, were selected ultimately for the computational fluid dynamics (CFD) and acoustic simulations respectively, as depicted in the Figures 6(a) and 6(b).

Figure 4.

The comparison between the simulated transmission loss (TL) obtained from the model constructed using the current steps in COMSOL and the experimental results.

https://journal.gpps.global/f/fulltexts/188265/JGPPS-00218-2023-01.04_min.jpg
Figure 5.

Mesh independence test. (a) Velocity profles at the x=D{res}/2 section of downstream combustor duct for the various CFD meshes. (b) Transmission loss for the various Acoustics meshes.

https://journal.gpps.global/f/fulltexts/188265/JGPPS-00218-2023-01.05_min.jpg
Figure 6.

The flow and acoustic meshes utilized for three-dimensional modeling of the coupling of a Helmholtz resonator and combustor. (a) The flow computational mesh. Meshc2 = 1,363,549. (b) The acoustics computational mesh. Mesha2 = 576,381.

https://journal.gpps.global/f/fulltexts/188265/JGPPS-00218-2023-01.06_min.jpg

Results and discussion

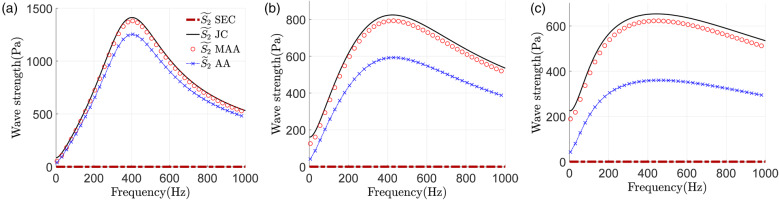
We now consider a test case to study the effect of the temperature difference between the HR and combustor on the acoustics inside the combustor. In this case, we make the assumption that the upstream and downstream sections of the combustor duct are both infinitely long, i.e. non-reflecting boundary condition. An incident wave p~1+=100Pa is introduced at the upstream section to excite the entire acoustic field within the combustor.

Comparisons with previous models are performed to validate the present model in the isothermal case. Other different acoustic boundary conditions are also can consider to our model. Maintaining the bias flow temperature T¯n=500K and the grazing flow temperature T¯1=1000K, we continuously increase bias flow Mach number M¯n. This is to make the mean bias flow no longer negligible compared to the mean grazing flow. Figures 7 and 8 show the theoretical and COMSOL numerical results for acoustic and transmission loss (defined as 20log10|p~1+/p~2+|) with the bias flow Mach numbers set to M¯n=0.03, M¯n=0.06, M¯n=0.09 (corresponding to m¯n/m¯1≈5.1%, m¯n/m¯1≈10.2%, m¯n/m¯1≈15.3%, respectively).

Figure 7.

Comparison of acoustic wave strength across various models and numerical results. (a) M¯n=0.03,m¯n/m¯1≈5.1%. (b) M¯n=0.06,m¯n/m¯1≈10.2%. (c) M¯n=0.09,m¯n/m¯1≈15.3%.

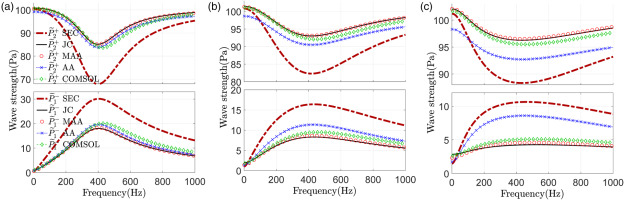
https://journal.gpps.global/f/fulltexts/188265/JGPPS-00218-2023-01.07_min.jpg
Figure 8.

Comparison of downstream duct transmission loss across various models and numerical results. (a) M¯n=0.03,m¯n/m¯1≈5.1%. (b) M¯n=0.06,m¯n/m¯1≈10.2%. (c) M¯n=0.09,m¯n/m¯1≈15.3%.

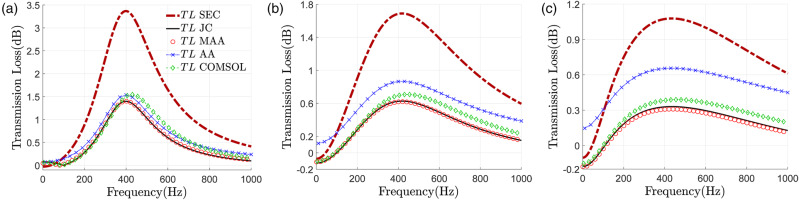
https://journal.gpps.global/f/fulltexts/188265/JGPPS-00218-2023-01.08_min.jpg

From Figures 7(a) and 8(a), it can be seen that when m¯n/m¯1≈5.1% the prediction results of the AA, MAA, and JC theoretical models are consistent with COMSOL, indicating that the difference in the mean flow parameters before and after crossing the HR can still be ignored, and its effect on the acoustics is negligible. From Figures 7(b) and 8(b), it can be observed that when m¯n/m¯1≈10.2%, the predicted results of the AA model differ significantly from those of the MAA and JC models, and the relative error of the peak transmission loss of the AA model based on COMSOL reached 23%, indicating that ignoring the difference in mean flow parameters before and after the HR will affect the accuracy of the results. The numerical results validate the accuracy of the MAA and JC models. When further increasing the bias flow Mach number to m¯n/m¯1≈15.3%, the predicted relative error in transmission loss by the AA model is further amplified, reaching approximately 70%, as shown in Figures 7(c) and 8(c). The results of the SEC model demonstrate that these two temperature differences in all three configurations of bias flow Mach numbers should not be overlooked; its predicted outcomes are significantly different from the current model’s predictions. It can be clearly seen that the present MAA model predicts results that are essentially consistent with the numerical simulation in all three cases, with negligible differences. This difference arises from the intrusion of hot grazing flow in the HR neck region in the COMSOL model, leading to an increase in the mean neck temperature. We found that by adjusting the neck input temperature of the theoretical model to match that in COMSOL, the results of the theoretical model perfectly align with those of the COMSOL model. The AA model accounts for the temperature difference in the mean flow between HR and combustor but neglects temperature variations in the mean flow within the combustor upstream and downstream, which can be referenced to our previous work (Gan and Yang, 2022), so cannot predict the correct results when M¯n is large. The JC model (Yang and Morgans, 2017) correlates the perturbations upstream and downstream via a scattering matrix and, being similar to the present model, can capture the effects of two temperature differences. However, unlike the AA and MAA models, it fails to provide a satisfactory physical interpretation. The SEC model (Dupére and Dowling, 2005) which assumes continuity of stagnation enthalpy between the up- and downstream regions of the combustor, can not capture the two kinds of temperature difference.

The entropy wave strength can be defined as S~(x)=s~(x)(γ−1)ρ¯T¯, where s~=Cvp~/p¯−Cpρ~/ρ¯ represents the entropy disturbance. The predicted curve for the entropy wave strength are shown in Figure 9. Comparison of the AA model with MAA and JC reveals that neglecting the difference in the mean grazing flow across the HR underestimates the generation of entropy wave strength downstream of the combustor. The error of the AA model is small when M¯n=0.03, while for bias flow Mach numbers up to 0.09, the predicted value of the AA model is half of the MAA and JC models. The observed discrepancy is precisely ascribed to the first term within the parentheses of Equation (12). This term arises from the discontinuity in the mean stagnation enthalpy between the upstream and downstream sides of the combustor.

Figure 9.

Comparison of entropy wave strength across various models. (a) M¯n=0.03,m¯n/m¯1≈5.1%. (b) M¯n=0.06,m¯n/m¯1≈10.2%. (c) M¯n=0.09,m¯n/m¯1≈15.3%.

https://journal.gpps.global/f/fulltexts/188265/JGPPS-00218-2023-01.09_min.jpg

Conclusion

In this paper, we extend our previous work on the acoustic analogy (AA) model (Gan and Yang, 2022) and propose a new model, MAA. The new model incorporates the effects of temperature difference between the upstream and downstream sides of the combustor in addition to the previously considered effects of temperature difference between the HR and the combustor. While the AA model provides a reasonable explanation for the acoustic effects in the combustor produced by the HR with cooling flow, the new MAA model is more general and includes the discontinuity effects of the mean flow parameters between the upstream and downstream regions of the combustion chamber. Comparing the theoretical and numerical results obtained from the COMSOL simulation, we find that when the ratio between the mean bias mass flux and the mean grazing mass flux does not exceed 10% in this study, the discontinuity effects of the mean flow parameters inside the combustor significantly will have negligible impact on acoustic and entropy wave strengths in the combustor. When this mass ratio is relatively large, ignoring this effect would result in overestimating the transmission loss in the combustor duct and underestimating the entropy waves strength generated downstream of the combustor. Moreover, the error increases with the increase of the bias mass flow rate. Therefore, in some cases where a large bias mass flow rate is required, it is necessary to consider both the temperature difference between the HR and the combustor and the temperature difference between the upstream and downstream regions of the combustor.

Nomenclature

Cp

heat capacity at constant pressure, J/(K · kg)

Rgas

the perfect gas constant

KRt

Revised Rayleigh conductivity

δ(x)

Dirac’s delta function

D

Dimeter, m

L

Length, m

A

Cross-sectional area, m2

V

The volume of the HR cavity, m3

m

Mass flux, kg/s

f

Momentum flux, kg·m/s2

e

Energy flux, kg·m2/s3

E

Stagnation enthalpy, J/kg

p

Pressure, Pa

s

Entropy, J/(K·kg)

S

Entropy oscillations strength, Pa

t

Time, s

x

Axial location, m

T

Temperature, K

u

Velocity, m/s

c

Speed of sound, m/s

ω

Angular frequency, rad/s

ρ

Density, kg/m3

k

The wavenumber, m−1

M

Mach number

γ

Heat capacity ratio

Abbreviations

SEC

The Dupère and Dowling’s Stagnation Enthalpy Continuity model

JC

The Yang and Morgans’s Jump Condition model

AA

The Acoustic Analogy model

MAA

The Mean Acoustic Analogy model

Subscripts

n

Neck of the HR

v

Cavity of the HR

1, 2

Section number of the system (here a combustor duct)

Superscripts

+

Downstream propagation

−

Upstream propagation

′

Time domain oscillation

Overscripts

∼

Fourier amplitude of oscillation

–

Mean value