RTE in concentric cylindrical medium

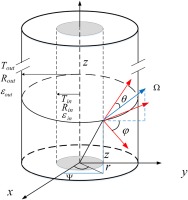
As shown in Figure 1, the present paper studies the radiation and coupled radiation-conduction heat transfer in cylindrical coordinate system. The θ is polar angle and φ is azimuthal angle. The absorbing, emitting and anisotropic scattering medium is filled in concentric cylinders where the subscripts in and out refer to the inner and outer wall, respectively.

Figure 1.

Physical model of concentric cylinders.

The RTE in one-dimensional cylindrical gray medium can be written as Modest and Mazumder (2021),

with the boundary conditions:

where I(r,Ω) is the radiative intensity at spatial position r along angular direction Ω; Ω(θ,φ)=erμ+eψη+ezξ=ersinθsinφ+eψsinθcosφ+ezcosθ is the angular direction described by polar angle θ and azimuthal angle φ; β=κa+κs is extinction coefficient in which κa and κs are absorption coefficient and scattering coefficient, respectively. S(r,Ω) is source term which is defined as,

where Ib is the black body radiative intensity. The scattering phase function Φ(Ω,Ω′) describes the probability of photon scattering from incident direction Ω′ to the direction Ω.

In this paper, the symmetry of one-dimensional cylinder is used. Therefore, the computational domains of 1D case are,

Discontinuous Galerkin method

The discontinuous Galerkin method (DG method) Cockburn (2003) combines features of the finite element and the finite volume framework. Unlike traditional continuous Galerkin method, the DG method works over a trial space of functions that are only piecewise continuous. This means the solution can possibly has a different values on the shared boundary of different elements. An alternative formulation, the so-called weak formulation, is used to get a representation as a piecewise polynomial, in which the polynomial is discontinuous at the element boundaries. The transport equation is taken as an example to introduce the implementation of DG.

First, the solution domain Rn is decomposed into Nel non-overlapping elements Eeln:

Then, we need to derive the weak form of the PDE Equation 5. Multiply both sides of Equation 5 by a differentiable test function v, and integrate the resulting equation over the space E to get,

using integration by parts,

where ∂E means the boundary of element E, n denotes the outward normal vector of the boundary. Equation 8 is referred as a weak formulation of Equation 5.

The calculation of DG is carried out on each element, and DG establishes a link between the values of solution in different elements only through flux on the boundary. Therefore, the numerical flux au¯ instead of au need to be introduced to exchange the information between different elements. In this paper, the classical up-winding scheme is considered, in which the numerical flux is modeled as,

where the operator {⋅} and [⋅] denote the mean value and the jump value of arguments across element boundary, respectively.

Here the superscript operator “+” and “−” denote the values at the boundary inside and outside element, respectively.

Spectral element discretization

In spectral element discretization Patera (1984), the nodal basis functions on each element are constructed by Chebyshev polynomial expansion. For one-dimensional case in standard computing domain [−1,1], the nodal basis functions are Lagrange interpolation polynomials through the Chebyshev–Gauss–Lobatto points αCGL,

After the construction of basis functions, quantity u to be solved in any position on element can be approximated as,

where Ne is the number of nodes in element E. the Γi is the the basis function of node i.

Discontinuous spectral element method discretization of RTE

In order to use DSEM to discretize RTE in cylinderical coordinate system, it is necessary to use the mathematical equivalent form instead of the usual form of the RTE given by Equation 1. However, as shown in Equation 1, there exists a minus sign ′−′ before the angular differential term ∂/∂φ in the RTE. This means there are two different mathematical equivalent forms for Equation 1. It is worth noting that it is critical to choose the proper mathematical equivalent form for the successful implement of DSEM. The two different kinds mathematical equivalent forms are:

where the dependences of I on r and μ have been omitted to simplify the expression.

Physical meaning of the two mathematical equivalent forms

As mentioned before, the computational domain of 1D case is: r∈[Rin,Rout],φ∈[0,π],θ∈[0,π2], which means η=sinθcosφ≥0 in the whole computational domain. After applying the DSEM to Form a (equation 13a) and Form b (equation. 13b), respectively, one can obtain:

(14a)

Forma∫EI[−μr∂Γ∂r−(−η)∂Γ∂φ+βrΓ]drdφdθ+∮∂Enr⋅(μr)IΓ¯dl+∮∂Enφ⋅(−η)IΓ¯dl=∫ErSΓdrdφdθ

(14b)

Formb∫EI[−μr∂Γ∂r+(η)∂Γ∂φ+βrΓ]drdφdθ+∮∂Enr⋅(μr)IΓ¯dl−∮∂Enφ⋅(η)IΓ¯dl=∫ErSΓdrdφdθ

It is obvious that the only difference between the two mathematical equivalent forms lies in the boundary integral term ±∮∂Enφ⋅(∓η)IΓ¯dl. Therefore, the influence of this boundary integral term ±∮∂Enφ⋅(∓η)IΓ¯dl need to be studied.

First, we consider Form a. For the case when nφ=−1 (Figure 2a), using up-winding scheme and substituting Equation 9, Equation 10 and nφ=−1 into boundary integral term, we can obtain,

Figure 2.

Diagram of φ boundaries. (a) boundary of nφ=−1. (b) boundary of nφ=1.

(15)

∮∂Enφ⋅(−η)IΓ¯dl=∮∂E(−1)⋅(−η){I}Γdl+∮∂E|(−1)⋅(−η)|[I]IΓdl=∮∂E(−1)⋅(−η)I+Γdl=∮∂Enφ⋅(−η)I+Γdl

The equation above means that I+ inside the element E as shown in Figure 2a is the upstream physical quantity. That is to say that radiative intensity with larger φ is the upstream and radiation with smaller φ is the downstream. The radiation propagates from larger φ to smaller φ.

For the case when nφ=1 (Figure 2b), Substituting Equation 9, Equation 10 and nφ=1 into boundary integral term, we can obtain,

(16)

∮∂Enφ⋅(−η)IΓ¯dl=∮∂E(1)⋅(−η){I}Γdl+∮∂E|(1)⋅(−η)|[I]IΓdl=∮∂E(1)⋅(−η)I−Γdl=∮∂Enφ⋅(−η)I−Γdl

The equation above means that I− outside the element E as shown in Figure 2b is the upstream physical quantity. In other words, radiation transfers from larger φ to smaller φ. In conclusion, the physical meaning of Form a is that radiation propagates from larger φ to smaller φ in φ direction.

Similarly, the physical meaning of Form b can be analyzed in the same way. For the case when nφ=−1, we can get,

(17)

−∮∂Enφ⋅(η)IΓ¯dl=−[∮∂E(−1)⋅(η){I}Γdl+∮∂E|(−1)⋅(η)|[I]IΓdl]=−∮∂E(−1)⋅(η)I−Γdl=−∮∂Enφ⋅(η)I−Γdl

The equation above means that I− outside the element is the upstream physical quantity. That is to say that the radiative intensity with smaller φ is upstream. Radiation propagates from smaller φ to larger φ.

When nφ=1, we will get,

(18)

−∮∂Enφ⋅(η)IΓ¯dl=−[∮∂E(1)⋅(η){I}Γdl+∮∂E|(1)⋅(η)|[I]IΓdl]=−∮∂E(1)⋅(η)I+Γdl=−∮∂Enφ⋅(η)I+Γdl

The equation above means that I+ inside the element is upstream physical quantity in φ direction and radiation propagates from smaller φ to larger φ.

In conclusion, the physical meaning of Form b is that in φ direction radiation propagates from smaller φ to larger φ. This conclusion means that the physical meanings of Form a and Form b are just the opposite. Therefore, we need to reveal the real physical scene of radiation propagation in cylindrical coordinate system, and then determine which mathematical equivalent form should be chosen in this paper to implement DSEM.

Radiation propagation in cylindrical coordinate system

In angular direction φ, there exists an implicit relationship between the “upstream” and “downstream”. The angular computational domain in the cylindrical symmetric RTE is φ∈[0,π]. Figure 3a and 3b present two typical propagations of radiation to clarify the implicit relationship of the “upstream” and “downstream” in angular φ direction. It is obvious that the position with larger φ is the “upstream” while smaller φ is the “downstream”, radiation propagates from larger φ to smaller φ.

Figure 3.

The two typical propagations of the radiation in r−φ plane. (a) typical propagation path 1 (b) typical propagation path 2.

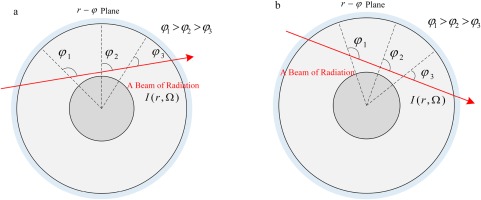
It can be seen that the physical meaning of Form a is consistent with the physical reality of radiation propagation in the cylindrical coordinate system while the physical meaning of Form b is just the opposite. Therefore, the Form a (equation 14a) is the mathematical equivalent which we should choose in this paper while the Form b is not allowed to be used.

Spectral element method discretization of energy equation

For copuled radiation-conduction heat transfer problem in cylindrical coordinate system, different from the RTE which involving three-dimensional r−φ−θ domain, the one-dimensional energy equation with radiative source term is,

where k is thermal conductivity, T∗ is the temperature value of the latest iteration step.

Since the coupling between the energy equation and the equation of radiation transfer is highly nonlinear due to the relationship between Ib and the fourth power of temperature T, it is necessary to employ iterative method to solve the copuled radiation-conduction problem.

The energy equation Equation 19 is a classical elliptic equation. Therefore, a good result can be obtained by directly using the spectral element method (SEM) without introducing discontinuous Galerkin scheme. The mesh of SEM adopts the same number of elements and nodes as DSEM to avoid using two sets of computational grid which would cause the increase of computational cost and the decrease of accuracy. Applying the SEM to Equation 19, we can obtain:

The extension to 2D cylindrical system

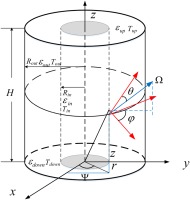
Figure 4 depicts the 2D cylindrical system, the z direction need to be considered compared with 1D case. Therefore, from the mathematical point of view, the radiation heat transfer problem in 2D cylindrical system considered here is actually 4D case, the polar angle θ, azimuthal angle φ, spatial r and z.

Figure 4.

Physical model of 2D concentric cylinders.

Grid independence tests

The grid independence tests are conducted in this section. Radiative equilibrium situation is considered firstly, the radius ratio of concentric cylinder Rin/Rout=0.1, the outer wall remains cold, i.e. Tout≡0. The cylinder is filled with isotropically scattering media, because of the isotropic scattering, the scattering albedo does not change the distribution of radiative heat flux. Figure 5a gives the change of dimensionalless radiative heat flux qr∗=qr/σTin4 at the inner wall with extinction coefficient β when the number of nodes in the element Mr×Mφ×Mθ changes and the number of elements is fixed as Nr×Nφ×Nθ=8×8×8. The results in Figure 5a show that when Mr×Mφ×Mθ is larger than 8×8×8, the dimensionalless radiative heat flux qr∗ at the inner wall remains almost unchanged and in consistent with the result of the modified discrete coordinate method (MDOM) Mishra and Krishna (2011). Figure 5b presents the changing trend of qr∗ at the inner wall with extinction coefficient under the condition that the number of nodes in the element Mr×Mφ×Mθ=8×8×8 remains constant and the number of elements Nr×Nφ×Nθ changes. It can be seen that, the results are not in good agreement with the those in reference when Nr×Nφ×Nθ=2×2×2. With the number of elements increases from 3×3×3 to 6×6×6, the results agree well with reference and remain basically unchanged.

Figure 5.

The grid independence test. (a) the number of nodes in element Mr×Mφ×Mθ. (b) the number of elements Nr×Nφ×Nθ.

Radiation heat transfer in 1D cylindrical system

Note that the radiative equilibrium problem is already considered in the grid independence tests above, then another typical radiation heat transfer problem, non-radiative equilibrium case would be numerically analyzed in the following section.

For non-radiative equilibrium problem, the radiative participating medium is the radiation heat source. The concentric cylinder boundaries remain cold, i.e. Tin=Tout=0. The change of dimensionalless radiative heat flux qr∗ at both inner and outer wall with extinction coefficient β are depicted in Figure 6. In Figure 6a, the scattering albedo ω=0. And it can be seen that for a given value of β, the dimensionalless radiative heat flux qr∗ increases with the increase of radius ratio Rin/Rout in both inner and outer wall. In Figure 6b qr∗ decreases all the time when scattering albedo ω becomes larger. This is because the larger ω means more energy the medium would be scattered, and the radiative heat flux would decrease consequently. It is obvious that the numerical results of DSEM are in good agreement with the results in reference Mishra and Krishna (2011) for the non-radiative equilibrium problem.

Figure 6.

The influence of extinction coefficient β on dimensionless radiative heat flux qr∗. (a) different radius ratio Rin/Rout. (b) different scattering albedo ω.

Coupled radiation-conduction heat transfer in 1D cylindrical system

Table 1 shows the dimensionless total heat flux in inner wall qt∗(Rin) and outer wall qt∗(Rout) under conditions of different conduction-radiation parameter Ncr and different scattering albedo ω for the case Rin/Rout=0.5, ε_in = ε_out = 1, Tout/Tin=0.5 and β=1. The mesh used in this case is Nr×Nφ×Nθ=16×8×8 and Mr×Mφ×Mθ=5×5×5. It can be seen that the numerical results of DSEM-SEM used in this paper are basically consistent with the results of FCT and SCM, Thus, it is verified that the DSEM-SEM can correctly solve the coupled radiation-conduction problem in one-dimensional cylindrical system.

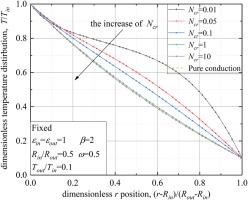
After verifying the feasibility of DSEM-SEM scheme, we study the effects of conduction-radiation parameter Ncr on dimensionless temperature for coupled radiation-conduction problem. Figure 7 gives the dimensionless temperature distribution for different Ncr and the case of pure heat conduction. It can be seen that, when Ncr is relatively small, the dimensionless temperature has an obvious nonlinear distribution. However, with the further increase of Ncr, the dimensionless temperature distribution tends to be linear and gets closer to the profile of pure heat conduction.

Figure 7.

Effects of conduction-radiation parameter Ncr on dimensionless temperature distribution.

The conduction-radiation parameter Ncr=kβ/4σTref3 is defined as the ratio of conductive heat transfer and radiation heat transfer. It is obvious that, for a large value of Ncr, conduction plays a dominant role in coupled heat transfer problem. On the contrary, a small value of Ncr means radiation becomes much more pronounced. For the conduction-dominated problem, the dimensionless temperature tends to be linear while the dimensionless temperature tends to be nonlinear for the radiation-dominated problem. Thus, with the increasing of conduction-radiation parameter, the distribution of dimensionless temperature changes from nonlinear to linear.

The radiation and coupled radiation-conduction heat transfer in 2D cylindrical system

The radiation heat transfer in 2D cylindrical system

The non-radiative equilibrium is considered in 2D cylindrical system. The inner, outer, up and down walls of the 2D cylinder are all cold, i.e. Twall≡0. And all of the four walls are black diffusive boundaries. The height of cylinder is H=Zup−Zdown=2, Rout=1, radius ratio Rin/Rout=0.5. Figure 8 shows the dimensionless radiative heat flux along the axial z direction at the outer wall of a two-dimensional cylinder with various radiative heat transfer parameters.

Figure 8.

The influence of different radiative heat transfer parameters on dimensionless radiative heat flux qr∗. (a) extinction coefficient β. (b) scattering albedo ω.

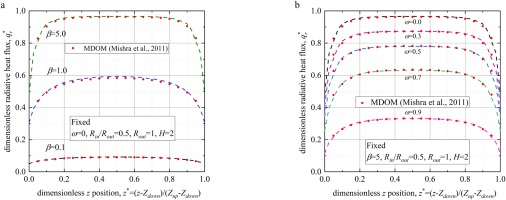
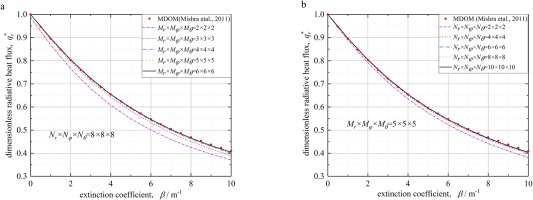
Figure 8 shows the results of DSEM in the 2D cylinder case, the results are compared with those of modified discrete coordinate method (MDOM) in ref. Mishra et al. (2011). The comparison shows that in various cases, the results of DSEM are all in good agreement with those in reference, which verifies the feasibility of DSEM in two-dimensional cylindrical system. The effects of different radiative heat transfer parameters on dimensionless radiative heat flux qr∗ will be further analyzed.

Figure 8a shows the influence of extinction coefficient β on qr∗ when the scattering albedo ω=0 and radius ratio is set to Rin/Rout=0.5. It can be seen from the figure that with the increase of extinction coefficient β, the qr∗ increases significantly. This is because when the scattering albedo ω is fixed, the larger the extinction coefficient β means there would be more interaction between photon and medium.Therefore, the radianve heat flux qr∗ would be larger with the increase of β.

The influence of scattering albedo ω on dimensionless radianve heat flux qr∗ is given in Figure 8b, in which the extinction coefficient β and radius ratio Rin/Rout remain unchanged. The scattering albedo ω represents the degree of scattering. As scattering albedo approaches 1, the scattering becomes more stronger, and the medium would absorb less radiative energy. Therefore, when other parameters remain unchanged, the increase of scattering albedo ω would lead to a decrease trend of radiative heat flux. And this trend is reflected in Figure 8b clearly.

Coupled radiation-conduction heat transfer in 2D cylindrical system

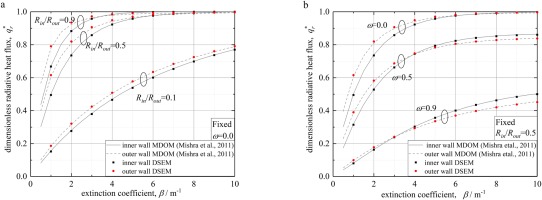
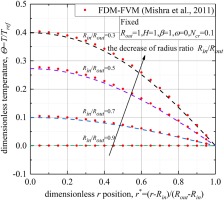
In this chapter DSEM-SEM scheme would be extended from 1D cylinder case to solve the coupled radiation-conduction problem in 2D cylindrical system. The results solved by Finite Difference Method-Finite Volume Method (FDM-FVM) in ref. Mishra et al. (2011) are also presented for comparison, in which the radiative intensity are obtained by FVM while the energy equation is solved by FDM.

In this case, the height of 2D cylinder H=Zup−Zdown=1, Rout=1, the medium inside cylinder is isotropic scattering. Radiative heat transfer parameters are: extinction coefficient β=1, scattering albedo ω=0. The outer and up wall are cold wall Tout=Tup=0 while Tdown=100=Tref, the inner wall is adiabatic boundary, which means ∂T/∂r=0.

Figure 9 shows the influence of radius ratios Rin/Rout on dimensionless temperature Θ of 2D concentric cylinder when the conduction-radiation parameter Ncr=0.1 remains unchanged. The temperature distribution at axial central plane z=(Zdown+Zup)/2 is given. It can be seen that as Rin/Rout decreases, the dimensionless temperature at the axial central plane gradually increases. This is because the space inside the cylinder becomes larger when Rin/Rout decreases, and more heat can be transferred from the down wall Tdown with high temperature to the axial central plane, which causes the increase of dimensionless temperature in this plane. And it can be expected that the temperature distribution would reach the highest when the Rin/Rout=0 (i.e. a solid 2D cylinder), and the corresponding Θ at r∗=0 in axial central plane would be 0.5.

Figure 9.

Radial distribution of dimensionless temperature Θ at the axial central plane z=(Zdown+Zup)/2.