Introduction
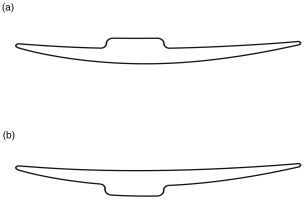
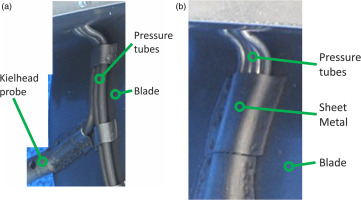
Although more accurate numerical models are increasingly used in numerical flow simulation due to decreasing computational costs in the last decades, experimental tests on multistage compressor rigs are still necessary to validate the numerical predictions. In order to measure quantities such as total temperature or total pressure within the rig, Kielhead probes, which are attached to the leading edges of the stators, are often used (see Figure 1a). The static profile pressure distribution on the surfaces of the stator blades is measured by static pressure taps. In particular, it is in the rear stages of the compressor that the tubes connecting the probes or the taps to the measuring devices outside the rig cannot be routed inside the blade for structural strength reasons. Instead, the tubes are attached to the blade surface and sometimes covered with a thin sheet of metal (see Figure 1b). This inevitably leads to considerable changes in the blade geometry since the dimensions of the pressure tubes can be in the same order of magnitude as the blade thickness. As a result, this produces additional total pressure losses, which ultimately affect the measured efficiency of the rig. This efficiency deviates from the numerically calculated efficiency of a non-instrumented rig due to the effects of the intrusive measurement technique and so must subsequently be corrected to take this error into account.
Figure 1.
Pressure tubes on the surface of an axial compressor blade. (a) Connecting Kielhead probes. (b) Connecting static profile pressure taps.
The literature on this subject provides a number of insights into the effects of these pressure tubes when mounted on the surface of compressor and turbine blades. Most studies, however, have investigated pressure tubes in combination with airfoil probes at the stator leading edge, which makes separating the effects of these two blade modifications challenging. Ma and Jin (2016) conducted numerical and experimental tests on the effects of two airfoil probes with spanwise pressure tubes at various span- and chordwise positions on the pressure side of a compressor blade. All tests were conducted at low Reynolds and Mach numbers of 150,000 and 0.05 respectively. For the case which is most comparable to the setup we examined (case 348), they reported that the integral total pressure loss coefficient increased by approximately 90% when a pressure tube was placed at 30% of the chord length and two airfoil probes were added at 45% and 85% spanwise height. Although Ma and Jin did not specify the amount of total pressure loss generated by the tubes and probes individually, their data shows that wake regions unaffected by the two airfoil probes still exhibited an increased total pressure loss of approx. 60%. In a follow-up paper to this study, Ma et al. (2017) conducted additional RANS simulations at a higher Mach number of 0.7. The results showed that the flow on the pressure side separates from the blade surface upstream of the spanwise pressure tubes and subsequently reattaches downstream. The distance between the upstream separation and the pressure tube is approx. four times the pressure tube diameter while the distance between the pressure tube and the reattachment line is approx. 18 times the pressure tube diameter. A similar separation behavior was reported by Zhang et al. (2023), who added three airfoil probes (5% span, 50% span and 95% span) to the leading edge and a spanwise pressure tube at 50% chord length to the compressor cascade blade V103-220. This phenomenon contributes to an overall increase in the total pressure loss coefficient by approx. 20%. Compared to the total pressure loss increase reported by Ma and Jin (2016), this loss increase is moderate and results from the fact that a spanwise pressure tube is less critical when placed closer towards the trailing edge. It is not clear, however, in the study by Zhang et al. (2023) how much of this total pressure coefficient increase can be attributed to the presence of the spanwise pressure tubes, since the interaction of the vortices induced by the airfoil probe with the separated regions and the corner vortices is highly complex.
As far as we know, only Chernoray et al. (2010), and Lalit et al. (2010) examined the effects of spanwise bumps on the suction and pressure side of turbine blades as part of their work on surface non-conformances caused by welding traces. The size of the surface non-conformance investigated was chosen as being 20% of the blade maximum thickness, which is smaller than the pressure tubes examined in our study, but still in the same order of magnitude. Chernoray et al. (2010) found that whenever such a surface non-conformance was placed on the suction side, a large open recirculation zone was formed. They identified the location of the welding trace at 20% chord length to be the most critical with an increase in the total pressure loss coefficient by a factor of almost ten. When placed at 30% chord length, the losses still increased by a factor of three. The pressure side proved to be insensitive towards any placement of a welding trace there. The authors also compared their experimental data to numerical RANS simulations and showed that only the
As this review of the existing literature shows, to date, there are no studies that consider the effects of spanwise pressure tubes on the surface of compressor blades in isolation. For the investigations described in this paper, we chose a particularly critical case, which arises when the tubes are mounted on the pressure or suction side of a blade of a rear high-pressure compressor stage. These modified blades were investigated experimentally in the linear cascade wind tunnel of the Institute of Jet Propulsion and Turbomachinery (IST) at the RWTH Aachen University. Numerical RANS simulations were used to examine the experimental results in more depth.
Methodology
Modelling of the pressure tubes
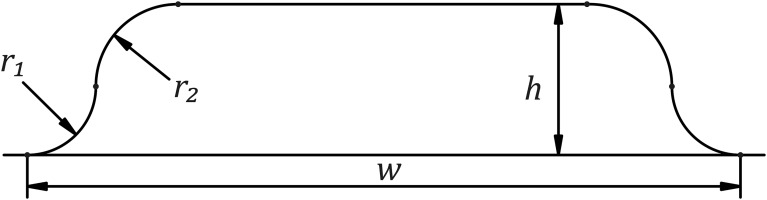
For the purpose of this study, we modeled the pressure tubes covered by a sheet of metal as a simplified bump. This bump, modeled on a flat plate for clarity, is presented in Figure 2. The variables h and w denote the height and width of the bump, respectively, while
Experimental setup
A high subsonic compressor cascade profile, which has already been used in previous investigations of our institute (Winter et al., 2013), was selected. The experiments were conducted at the linear cascade wind tunnel of the institute (see Figure 4). The air is supplied by a multistage radial compressor, which enables experiments in a Mach number range of 0.4 up to 0.85. Due to the closed-loop design, an engine-like Reynolds number between
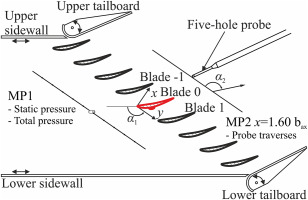
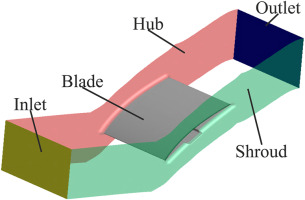
A cascade with only nominal blades is used as the reference case for this study. This configuration will be referred to as “clean blade” in the following. The periodicity of the flow is set for the clean blade cascade using the adjustable sidewalls and tailboards. To evaluate the influence of a spanwise bump, the central blade “Blade 0” is replaced by a modified blade with either a pressure-sided or a suction-sided bump, while all other blades remain nominal (see Figure 5). The additional losses generated by these bumps are found by comparing the modified cascade to the nominal cascade. The sidewall and the tailboard settings are not changed in relation to the clean blade cascade. All changes in the periodicity of the flow are therefore due to the influence of the bump. For the nominal cascade, only the wake of the central blade “Blade 0” is measured. In the case of the pressure-sided bump, the wake of the central modified blade is measured, while for the suction-sided bump, the pressure side-adjacent and suction side-adjacent blades (“Blade −1” and “Blade 1”) are measured as well. This configuration, in which there is only one modified blade surrounded by clean blades, is similar to a test rig which has only a few instrumented blades.
The profile loss is evaluated in terms of the local total pressure loss coefficient
The total inlet pressure
Here,
Since the blade geometry investigated is proprietary, all data on the total pressure loss coefficient
Numerical setup
To simulate the effects of the spanwise pressure tubes on the flow around the compressor blade, we used the code TRACE 9.4 (Turbomachinery Research Aerodynamic Computational Environment), which is developed by the German Aerospace Center (DLR) in cooperation with MTU Aero Engines. We solved the RANS equations with a finite volume scheme of second-order spatial accuracy by applying a MUSCL approach together with a central discretization of the viscous terms and Roe upwind-based convective flux difference splitting. In this study, the
Pressure-sided bump
In order to achieve mesh independence for every turbulence model, multiple mesh refinement studies were conducted. In the case of the pressure-sided bump, a single-passage approach (see Figure 7) was chosen, since the influence of the pressure-sided bump is mostly limited to the flow around the modified blade itself. Approximately 29 million cells were sufficient for the pressure-sided bump to achieve mesh independence with regard to the integral total pressure loss coefficient
Table 1.
Integral total pressure loss coefficients resulting from the mesh independence.
| Pressure-sided bump | Suction-sided bump | ||||
|---|---|---|---|---|---|
| Cells [*106] | Cells [*106] | ||||
| SST | SST | ||||
| 3.97 | 2.82 | 2.27 | 35.06 | 4.65 | 3.84 |
| 22.12 | 2.77 | 1.85 | 52.70 | 3.69 | 3.85 |
| 29.48 | 2.85 | 2.14 | |||
| 53.03 | 2.89 | 1.93 | |||
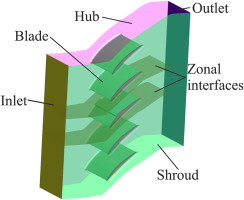
In the experiment performed, only the central blade of the cascade was modified, while all other blades were identical to the nominal blade. In the numerical simulations, however, this setup cannot be implemented due to the periodic boundary conditions in the pitch direction. A single-passage simulation here is equivalent to an infinite cascade where each blade is modified. In the case of large-scale flow separation, however, this approach is of limited value because the modified blade can influence the adjacent nominal blades. In order to verify whether there is influence from the neighboring blades and, if so, how large their influence is, simulations containing several passages were performed. In these multi-passage simulations, periodic boundary conditions were still used, but only the central blade was modified, so that the numerical model is equivalent to an infinite cascade in which only every n-th blade is modified. Since the adjacent nominal blades could be resolved using a much coarser mesh, they were connected to the mesh of the modified blade via non-matching zonal interfaces (see Figure 8 for the five-passage model).
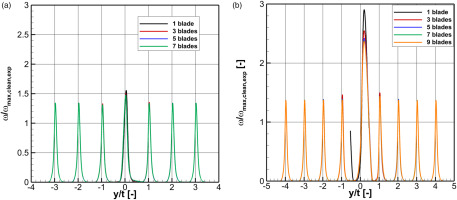
For the pressure-sided bump, four setups were investigated using 1, 3, 5 and 7 blades respectively. In these setups, only the central blade was modified. Figure 9a shows the resulting total pressure loss coefficient distribution in MP2, normalized by
Suction-sided bump
For the suction-sided bump, the mesh independence study was conducted with a domain consisting of five blades to account for the effects of the suction-sided bump on the adjacent blades. For the same reason, in the case of the suction-sided bump, the integral pressure loss coefficient
In order to check how many blades have to be included in the numerical domain to capture the effects of the adjacent nominal blades, we simulated models with 1, 3, 5, 7 and 9 blades respectively. The domain containing five blades is shown in Figure 8) as an example. In Figure 9b, the corresponding normalized total pressure loss coefficient distributions are shown. This plot clearly demonstrates, that the result of the setup with one blade only differs significantly from all other simulations, which is why this setup was not considered appropriate for this case. What is also evident is that the suction-sided bump influences not only the losses generated by the central blade, but those of the adjacent blades too. For the suction-sided pressure tubes therefore, we integrated the total pressure loss over the central three blades. We found that by simulating five blades, the integral total pressure loss coefficient deviated by 0.03 from the model with nine blades for both turbulence models. This deviation is in the same order of magnitude as the measurement uncertainty. The data can be found in Table 2, normalized by the experimental value for the integral total pressure loss coefficient of the central three blades of an unmodified cascade
Results and discussion
Clean blade
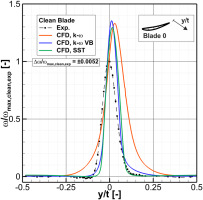
Before discussing the results of the modified blades, we first evaluate the performance of the CFD solver in the case of the clean blade by comparing the local and the integral total pressure loss coefficient to the experimental data. Figure 10 shows the normalized local total pressure loss coefficient for the experiment as well as the simulation results using the
Pressure-sided bump
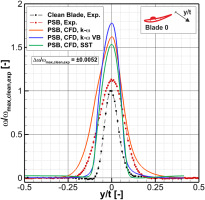
To evaluate the additional total pressure losses caused by the pressure-sided bump, we investigated the total pressure loss coefficient in the wake of the modified blade. As the CFD results indicate that most of the additional total pressure losses are generated in the wake of the modified blade, the wakes of the adjacent blades have not been investigated further in this study. To improve the comparability of the wakes and to eliminate the influence of the single-passage model on the flow turning, all wakes were centered with regard to their loss maxima. Figure 11 shows the experimental local total pressure loss coefficient for both the modified and the clean blade, as well as the numerical results of a single-passage simulation with a pressure-sided bump for the different turbulence model settings mentioned previously. When comparing the two experimental data, we find that the wake of the modified blade is wider than that of the clean blade and the peak is approx. 12% higher. By calculating the integral total pressure loss coefficient, we can observe that the PSB leads to an increase in
Table 4.
Normalized integral total pressure loss coefficient of the PSB blade.
| Experiment | 1.90 | 1.00 |
| CFD | 1.54 | 1.50 |
| CFD | 1.81 | 1.04 |
| CFD SST model | 1.77 | 1.02 |
The
Using surface oil flow visualization, we further analyzed the flow distortions caused by the PSB on the surface of the pressure side. The resulting oil flow pattern was then compared to the numerically obtained wall stream lines for the
Figure 12.
Oil flow visualization with overlaid wall streamlines for the PSB blade. ①: leading edge, ②: rising flank, ③: falling flank, ④: trailing edge. (a) Wall streamlines of k − ω
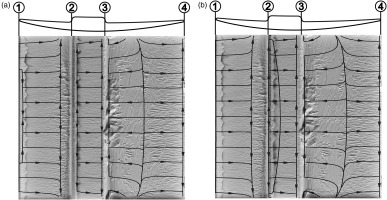
Figure 13.
Normalized Mach number distribution in midspan of the PSB blade. (a) k − ω
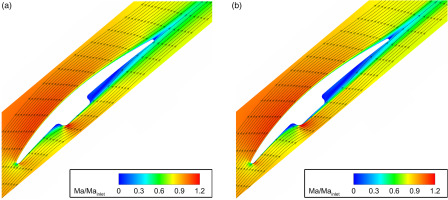
In conclusion, the numerical simulations are able to capture the trends of the experiments quite well. All turbulence models lead to a considerable increase in the integral total pressure loss coefficient, ranging from an increase by a factor of 1.54 to 1.81 caused by the PSB. The comparison between the oil flow visualizations and the numerically determined wall stream lines further demonstrates that the general flow physics is satisfactorily reproduced. Only the local distributions of
Suction-sided bump
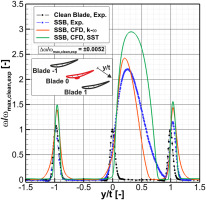
Analogous to the pressure-sided bump, Figure 14 shows the local total pressure loss coefficient for the blade modified with a suction-sided bump (SSB) and the clean blade for both the experimental and numerical results. As previously discussed, a domain with five blades was used to simulate the flow. As the SSB only significantly influences the losses generated in the central three passages, those results are shown in Figure 14. Again, all wakes were centered with regard to the experimentally determined wake center. The
From Figure 14, it is immediately apparent that the losses caused by the SSB are much larger than those caused by the PSB. Compared to the clean blade, the peak value of the suction-sided bump is 2.2 times larger. The flow deflection is reduced, as shown by the positive y-shift of the wake. Furthermore, the wake is much wider and extends into the wake of the adjacent blade, which can be seen by the fact that
Table 5.
Normalized integral total pressure loss coefficient of the SSB blade.
| Experiment | 4.10 | 1.00 |
| CFD | 1.97 | 0.90 |
| CFD SST model | 3.55 | 0.94 |
As seen for the pressure-sided bump, both the
To analyze the reason for the large difference between the two models and to quantify which of these describes the flow physics more accurately, we again performed an oil flow visualization. The results for the suction side with the bump are depicted in Figure 15, with overlaid wall streamlines for both turbulence models. On the suction side, there is no transition with a laminar separation bubble at the leading edge due to a favorable pressure gradient. Hoesgen (2019) determined that the transition occurs between 30% and 50% of the axial chord length, which in this case coincides with the location of the bump. The separation bubble upstream of the bump therefore triggers the transition from laminar to turbulent. At the top of the bump, the streamlines are curved toward the midspan and are not parallel to the inflow and the channel walls. Downstream of the bump, the backward-facing step again causes a separation bubble. Unlike for the pressure-sided bump, there is no reattachment line, indicating a fully separated flow with an open separation bubble extending beyond the trailing edge. In the vicinity of the bump, large amounts of paint accumulate near the cascade walls.
Figure 15.
Oil flow visualization with overlaid wall streamlines for the SSB blade. ①: leading edge, ②: rising flank, ③: falling flank, ④: trailing edge. (a) Wall streamlines of k − ω
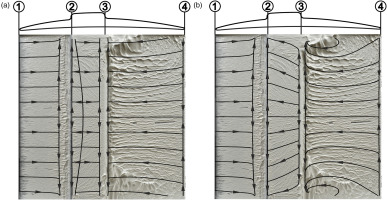
The area upstream of the bump is predicted similarly by both models, correctly predicting the separation bubble at the forward-facing step. However, the results for the surface of the bump and downstream of the bump differ significantly. A small closed separation bubble is present for the
The difference between the
Figure 16.
Normalized Mach number distribution in midspan of the SSB blade. (a) k − ω
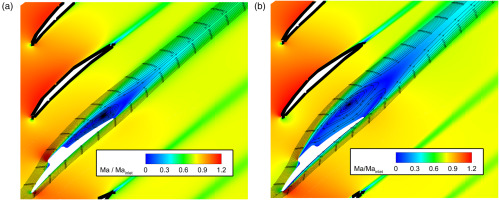
Overall, these experiments show that the addition of a bump to the suction side of a blade leads to an increase in the total pressure loss of factor 4.1 over three passages. This drastic increase is only reproduced by the SST turbulence model, which is likewise the only model able to simulate the detached flow over the bump correctly. Considering the challenging flow physics present in this case, the numerical simulation is able to reproduce the experimental results with good accuracy.
Conclusion
In this paper, we presented an experimental and numerical evaluation of the influence of pressure tubes on the pressure and suction side of a compressor stator blade. We modelled the pressure tube geometry as a simplified bump mounted on the blade surface. When a bump was placed on the pressure side, the integral total pressure loss was increased by a factor of 1.9. All three turbulence models (
In practice, this study shows that the presence of such pressure tubes can alter the measurement data of both the Kielhead probes and the static profile pressure taps. The latter are expected to be highly sensitive to even minor changes in the flow field. As a result, the measured profile pressure distribution is likely to differ from the pressure distribution of a clean blade. In future work, we plan to integrate static pressure taps into the modified blades to measure the altered pressure distribution. Furthermore, we will investigate different pressure tube configurations by varying the geometrical dimension of the bump.
Nomenclature
Total pressure loss coefficient (−)
Integral total pressure loss coefficient (−)
Axial chord length (mm)
Mach number (−)
Static pressure (Pa)
Total pressure (Pa)
Reynolds number (−)
Pitch (mm)
Pitchwise coordinate (mm)
IST
Institute of Jet Propulsion and Turbomachinery
MP
Measuring plane
PSB
Pressure-sided bump
SSB
Suction-sided bump
VB
Viscous Blending