Introduction

The development of innovative energy conversion and propulsion systems based on turbomachines requires equally innovative design methods with improved accuracy and capable of investigating wide and unexplored design spaces. Traditional design methods are based on company proprietary correlations used in the early conceptual/preliminary design phases, that are often unable to provide enough accuracy to remove substantial safety margins. Typical examples of legacy methods can be found in Wisler et al. (1977) and Craig and Cox (1970–71) for compressors and turbines respectively. Such design margins measure the “uncertainty” of predictions, reported in both Wisler et al. (1977) and Craig and Cox (1970–71) in the validation section, and are expected to be narrowed when moving to the “detailed” design phase, usually aided by differential methods, like CFD, structural mechanic analysis, chemistry and sometimes driven by multi-objective optimization algorithms as illustrated in (Astrua et al., 2012). Such methods rely on simplified models that attempt to reduce the computational effort (see for example RANS v/s LES or DNS for aero and aeromechanics, or full kinetic models v/s simplified flamelet models for combustion modelling) especially when running computer driven optimizations that may require thousands of iterations. Modelling assumptions introduce additional uncertainties that do require the adoption of design margins that may prevent a deep design optimization. Nevertheless, turbomachinery design is fairly mature, and it is based on a variety of data, like scaled down component tests, full engine field data, and computer simulations of material and fluid properties, aerodynamics, aeromechanics, combustion, rotor-dynamics and many others. The heterogenous nature of such large data sets, that are characterized by different levels of resolution (in space and time), accuracy, availability, and operating conditions, poses severe challenges to whoever may try to reconcile such a variety of data into a design system. At the same time, this gives numerous opportunities for the use of data-driven design methods such as machine learning, see (Michelassi, 2018). Machine learning is a type of Artificial Intelligence (AI) that leverages algorithms to find structure within data, as illustrated by (Brunton et al., 2020). This paper will focus on three opportunities that are transitioning from the academic realm to commercial relevance: (i) sequential learning for accelerated materials development and process optimization; (ii) co-optimization of materials and part performance; (iii) data-driven physics models applied to the effects of turbulence. Finally, as the key to machine learning is data sets availability, the paper also discusses data management, one of the underlying challenges that needs to be addressed to take full advantage of the emerging artificial intelligence methods based on machine learning.

Sequential learning for accelerated materials development

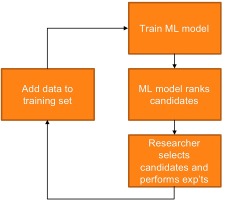
Energy conversion thermodynamic cycle efficiency calls for high operating pressures and temperatures. The resulting thermal and mechanical loads to stationary and rotating parts often require design compromises that erode either the performance or availability or increase cost. Recently, new materials have been applied to aircraft engines, like composite fan blades of the GE90–115B engine (GE Aviation, 2015), to reduce weight and allow tall blades with reduced pull, or ceramic matrix composites (CMC) parts in the hot-gas-path of gas turbines, as described in an early technical assessment by (Ohnabe et al., 1999), to allow a reduction in cooling flows at firing temperatures often above conventional material limits. Fink et al. (2010) worked on the design of superalloys capable of withstanding high gas temperatures while trying to reduce the rhenium content, a rare and costly component. Aeromechanics issues have also been addressed by unconventional approaches, as described by (Patsias, 2008) who investigated damping coatings properties as an alternative to more costly materials. The recent advances in additive manufacturing offers opportunities and challenges, while requiring the design of materials suited for the new process, as discussed by (Attallah et al., 2016). In short, the open literature offers many examples of both Academia and Industry efforts in the exploration of coatings, composite materials, or new alloys applicable to different sections and components of turbomachinery. Gas turbines design challenges in particular are driven by high temperatures, like in the turbine hot-gas-path, or high fatigue strength, like in any stator-rotor interaction for both compressors and turbines, and corrosion/erosion-resistance, like in parts exposed to dust, sand, and or combustion generated deposits. New materials development can take years to decades because of the high cost of manufacturing and testing as well as the highly iterative nature of the process. Machine learning can be used to reduce the number of experimental trials required to develop new high-performance materials. The sequential learning approach relies on first training a machine learning model on existing data, creating a mapping from composition and processing to performance properties. This model is then paired with a sampler or optimization routine that can explore a design space of potential candidate materials to rank the candidate materials. The candidate materials might be ranked based on highest predicted performance, maximum prediction uncertainty, or some other combination of exploratory versus exploitative acquisition function as discussed by (Ling et al., 2017). The researcher can then choose which experiments to run from the list of top ranked candidates, combining their scientific expertise with the machine learning model's suggestions. Once these experiments are performed, the data are added back into the training set so that the machine learning model can learn and suggest a new set of top ranked candidates for trial. This workflow (Figure 1) enables the combination of scientist expertise with data-driven models with the goal of systematically reducing the number of experimental trials required to find materials that meet specifications.

Figure 1.

Schematic of sequential learning process.

(Ling et al., 2018) demonstrated how a sequential learning approach could apply to several materials classes of relevance to the turbomachinery community: the development of corrosion-resistant and machinable aluminium alloys, nickel superalloys with high stress rupture time, and functional shape memory alloys with tuned transition temperatures. Related approaches have been used to explore thermoelectric materials (Gaultois et al., 2016), electronic materials (Lee et al., 2016), Heusler alloys (Olynyk and Mar, 2018), and other materials classes (Ramprasad et al., 2017). Gaultois et al. (2016) were able to use machine learning-based screening of 25,000 potential thermoelectric materials to uncover a new set of thermoelectric, Re12Co5Bi (RE = Gd, Er), that was experimentally confirmed to have low thermal conductivity, high electrical conductivity and a moderate Seebeck coefficient, that measures a thermoelectric voltage across a material induced by a temperature difference. This example shows the dual promise of machine learning-based approaches: the ability to rapidly screen a large number of potential candidates to uncover unusual or surprising high-potential candidates.

Another area of increased interest in turbomachinery is the development of new alloys that are compatible with additive manufacturing. These alloys must retain excellent mechanical properties despite the melting processes involved in additive manufacturing that can often lead to disadvantageous microstructures. Martin et al. (2017) demonstrated how data-driven methods could be combined with classic nucleation theory to explore millions of nanoparticle/powder combinations in the development of 3-D printable aluminium alloys. Nanoparticles that were compatible with each alloy were screened based on matching lattice spacing and density. In all, more than 11 million combinations were screened using this algorithmic approach. Their work led to a registered additive manufacturing aluminium alloy for aerospace applications, and it is another demonstration of how machine learning can serve as an approach for finding the needles in the haystack.

Transfer learning is a key opportunity presented in sequential learning. In materials development, there are often several sources of data, some of them plentiful and others scarce. For example, simple tensile strength data for nickel superalloys may be plentiful, but stress rupture data is often scarcer because of the cost and time required for those tests. Similarly, corrosion and fatigue strength data are time-intensive to acquire. In transfer learning, a model trained on one data source is applied to improve the accuracy in predicting a different data source.

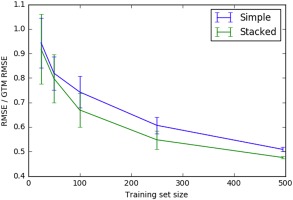
Hutchinson et al. (2017) demonstrated how transfer learning could be used in materials development to, for example, leverage plentiful density functional theory (DFT) data to improve model accuracy for experimental quantities. Figure 2 below shows the normalized model for two models: one that uses a transfer learning approach and one that does not. The model using a transfer learning approach is a stacked model that first predicts the DFT band gap, and then uses that predicted DFT band gap as an input to predict the experimental band gap. This stacked model can therefore leverage plentiful DFT data to train the first stage of the model, thereby improving its ability to predict experimental band gap, the true quantity of interest. As Figure 2 shows, the stacked model requires significantly less experimental band gap training data to achieve the same model accuracy as the simple model. This example demonstrates how the transfer learning approach can reduce the number of expensive experimental trials required to build an accurate machine learning model. A similar transfer learning approach could be applied to the lifetime properties that are commonly of interest in turbomachinery applications to reduce the number of the most expensive experiments required to build accurate machine learning models.

Figure 2.

Normalized model error for a stacked model and a simple model for predicting experimental band gap. The stacked model has two stages: one to predict DFT band gap given chemical formula, and the second using the predicted DFT band gap and the chemical formula as the inputs to predict experimental band gap. The simple model goes directly from chemical formula to experimental band gap.

Co-optimization of materials and part performance

Another challenge in the turbomachinery industry bridges beyond materials development to part design. Part designers typically have to select from a catalogue of existing materials or go through a risky and lengthy process of setting new materials specifications and finding vendors who can meet them. One of the potential opportunities with data-driven models is bridging this divide, so that part designers can design not only with existing materials, but also with some information on what new materials performance might be achievable. With this information, the part geometry could be co-optimized with the materials performance achievability in order to best hit performance, manufacturability, and testing targets.

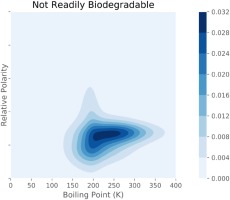
Recently, (Peerless et al., 2020) demonstrated how machine learning models could be used to assess not only single materials candidates, but also whole design spaces of candidates to determine the predicted achievable performance. Figure 3 shows a visualization of this design space evaluation approach, in which Peerless et al. investigated the predicted achievable performance across a design space of non-biodegradable solvents. They were able to compare this predicted performance with a design space of biodegradable solvents to assess the trade-off of design constraints around biodegradability.

Figure 3.

Visualization of the Summed Probability Distribution (SPD) for a design space of non-biodegradable solvents. This visualization presents the predicted performance of an entire design space, considering uncertainty estimates, to show the predicted accessible performance regions. Reproduced with permission from authors from (Peerless et al., 2020).

With these approaches, it would be possible to co-optimize part performance with materials performance achievability. This technology is more nascent but has the potential to fundamentally change part design workflows. It would be particularly impactful in applications where the materials performance is of critical importance to overall part performance, such as in engine hot sections. In these regions, co-designing e.g. turbine blade geometry with materials performance could lead to more efficient and robust designs.

Data-driven physics models

Reynolds Averaged Navier Stokes (RANS) models have long been used in turbomachinery applications because of the excessive computational cost of using higher fidelity Large Eddy Simulation (LES) or Direct Numerical Simulation (DNS) approaches at full engine scale and Reynolds number. While all aero-thermal-mechanical design of turbomachines is heavily CFD assisted, RANS cannot be fully exploited due to some well-known and documented inaccuracies mostly related to the method to determine the impact of turbulence on the mean flow field, as documented in (Laskowski et al., 2016; Sandberg and Michelassi, 2019). The different components of a gas turbine are affected differently by RANS uncertainties. For example, RANS and URANS are generally unable to guarantee the degree of accuracy needed to drive the design of axial compressor operability envelopes, or combustion chamber dynamics, or high-pressure turbine cooling, as documented by (Tucker, 2011; Cozzi et al., 2017). The challenges of turbomachinery flows change across components, as described by (Sandberg and Michelassi, 2019) and by (Tucker, 2011). For instance, compressor and turbine flows are wall driven and statistically periodic in time, and therefore require massive wall resolution and large number of revolutions to get statistical convergence. Combustion chambers, and cooling channels, are wall bounded and can be considered statistically steady, that may require less wall resolution and shorter physical times, with additional challenges in presence of chemical reactions, and the consequent strong coupling between pressure-velocity and temperature.

LES, and DNS where possible, proved able to resolve physics and drive the correct interpretation of the flow field when an adequate grid resolution was guaranteed. The experience of the authors concentrates first on axial compressors, see (Leggett et al., 2018), where LES revealed a loss generation mechanism with significant deviations from what was predicted by URANS. In combustion chambers RANS and URANS are known to predict insufficient mixing and consequently an inaccurate heat release, while LES (see (Meloni et al., 2019)) was capable of predicting stable and unstable operating conditions of an annular industrial gas turbine combustor. High pressure turbines pose formidable challenges to simulations due to the combination of high-pressure and temperature, transonic speeds that concurrently give high Reynolds and Mach numbers. Therefore, DNS is limited to small portions of the geometry, as done by (Wheeler et al., 2016), who revealed a suction side perturbation propagation that was not captured by conventional Reynolds averaged methods, with a practical implication on the determination of the aerodynamic throat area. Low pressure turbines can be tackled with a reasonable computational effort due to the relatively low Reynolds and Mach numbers, below 3 × 10⁵ and 0.6 respectively. Therefore there are many examples of single airfoil up to 2D and 3D stage DNS and LES (see (Michelassi et al., 2003; Tucker, 2011; Sandberg and Michelassi, 2019)). What is probably most relevant for this gas turbine component is that DNS and LES could constitute a valid alternative to experimental measures and indicate valuable design trends as a function of essential design parameters, as demonstrated by (Michelassi et al., 2016) for the combined effect of flow coefficient and reduced frequency, and by (Pichler et al., 2018) for stator-rotor gaps. In parallel to this, the inaccuracy of URANS was analysed by (Pichler et al., 2016) who revealed serious fundamental weaknesses.

Two-equation turbulence models were originally developed for planar free shear flows and attached boundary layers and their validity is stretched to flow and geometry conditions far beyond their validation range, as documented by (Wilcox, 1988) and by (Patel et al., 1985). So, it is somewhat surprising how Reynolds averaged models most of the times ensure fair accuracies. Nevertheless, such accuracy is often insufficient to further improve the mature design of gas turbines, or to investigate drastically new design spaces. The excessive computational effort of DNS and LES for a typical design work together with the weakness of (U)RANS naturally suggests the use of highly resolved DNS and LES predictions to improve the quality of the less computationally demanding approach. Despite the fairly large number of new models, turbulence modelling has been stagnating in the last decades. Some attempts to use high-fidelity CFD to improve the accuracy of Reynolds Averaged approaches, like the cumbersome full-Reynolds stress models, were not successful, as documented by (Parneix et al., 1998) who tried to improve the closure of some fundamental terms with the aid of DNS. (Rodi et al., 1993) improved near wall two-equation modelling with the help of fully developed channel flow DNS but did not find any improvement when moving to complex flows. So, the availability of DNS and LES data alone, while ensuring accuracy and resolution unthinkable for measurements, did not automatically improve the accuracy of lower-order closures. Some attempts have been made to determine flow areas and patterns where RANS suffer by analysing modelling closures with DNS (see again (Parneix et al., 1998; Michelassi et al., 2015; Pichler et al., 2016)). Still, it was only with the aid of Machine Learning that it was possible to efficiently extract physic information from the large DNS and LES databases to improve lower order models, as illustrated by (Weatheritt et al., 2017), who explored the use Gene Expression Programming (GEP) (Ferreira, 2001) and Deep Neural Networks (DNN) (LeCun et al., 2015) to improve turbulence modelling constitutive laws.

While there exists a strong link between turbulent stresses and turbulent heat flux, as discussed by (Wissink et al., 2004), often machine learning is used to improve models for the two separately. (Sandberg et al., 2018) used GEP to improve heat transfer prediction in a fundamental trailing edge slot that mimics the geometry and aerodynamic conditions of a high-pressure-turbine trailing edge cooling ejection. LES generated a set of data that was used to develop and validate a new expression for the turbulent Prandtl number necessary to compute turbulent diffusion of heat, while keeping the Fourier expression for heat transfer linear. The machine learnt model by GEP introduces an algebraic expression for the turbulent Prandtl number to correct the heat flux expression as:

in which u′iT′¯ is the turbulent heat flux, μt is the turbulent viscosity, dT¯/dxi is the time averaged temperature spatial gradient, and PrtI is the expression for the turbulent Prandtl number that depends on the fundamental turbulence invariants, I, introduced by (Lumley, 1970). The results showed a drastic improvement of the match with the measured heat transfer with no significant computational overhead with respect to a conventional RANS calculation, as illustrated in Figure 4 in which the machine-learnt model with the algebraic expression for the turbulent Prandtl number outperforms the RANS prediction with constant Prt.

Figure 4.

Comparison of measured and predicted adiabatic effectiveness in a fundamental trailing edge slot representative of a High-Pressure-Turbine trailing edge, adapted from (Sandberg et al., 2018).

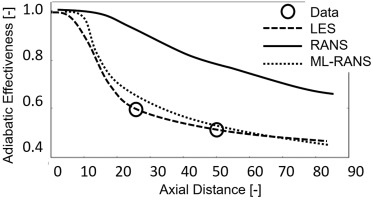
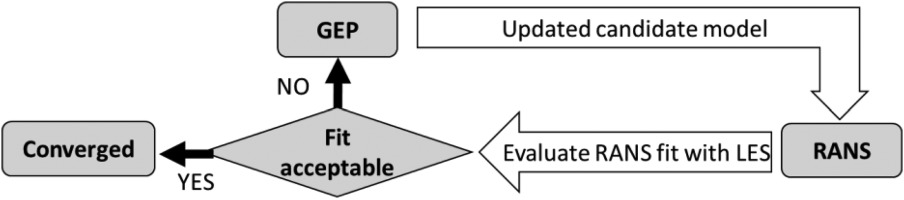
The method described in (Sandberg et al., 2018) develops the new constitutive law by using the frozen LES flow field since the modifications to the turbulent thermal diffusion model does not produce large changes to the velocity and pressure fields. In case the new model may cause significant changes into the flow field predicted by RANS, the training process must include a feedback loop that tests the new constitutive law by running a RANS simulation with the updated closure, rather than testing it by using the original LES flow field. This process is schematically illustrated in Figure 5, in which each new candidate model generated by GEP is tested by performing a RANS simulation, rather than comparing the turbulent shear stresses resolved in the LES database with those given by the new constitutive law computed with the LES velocity field.

Figure 5.

CFD-in-the-loop training of turbulence model based on GEP.

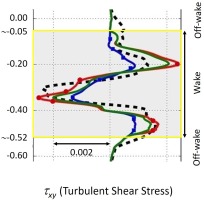
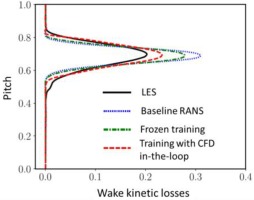
The introduction of the RANS feedback loop into the GEP training process addresses some of the weaknesses observed by (Weatheritt et al., 2017; Akolekar et al., 2019). In particular (Akolekar et al., 2019), observed that with unsteady stator rotor interaction where history effects do play a strong role, the training process with no direct RANS feedback could not always match LES very well, as illustrated in Figure 6, where GEP models trained by using different strategies still show visible deviations from LES in high-shear-gradient regions, that are important as they govern wake decay.

Figure 6.

Comparison of turbulence shear stress, τxy, pitchwise profile downstream a turbine airfoil, adapted from (Akolekar et al., 2019). Black dashed = LES, Blue = standard Boussinesq model, Red = GEP trained on individual phase-lock-averages, Green = GEP trained on gatherer LES discrete instants.

When the training process includes the RANS verification in the loop, the quality and the robustness of the ML-assisted model improves. This is described in detail by (Zhao et al., 2020), who developed a new non-linear constitutive law for the turbulent stresses suited for two-equation models to predict turbine wakes, as illustrated by Figure 7. Wake prediction is a fundamental miss of RANS that affects unsteady turbine performance and aeromechanics design, as indicated by (Michelassi et al., 2003) who compared LPT wakes predicted by DNS, LES, and URANS in presence of incoming wakes and concluded that LES was a fair replacement of the much more costly DNS, while RANS predicted wake shapes that differ substantially from the scale-resolving simulations.

Figure 7.

Low-Pressure Turbine exit wake predictions, adapted from (Zhao et al., 2020). Black = High-fidelity LES, Blue = standard Boussinesq model, Green = GEP trained with frozen flow field from LES, Red = GEP trained with RANS in the loop.

GEP provides an analytic expression of the closure model. An alternative approach is to use a Deep Neural Network (DNN), as illustrated by (Ling et al., 2016a,b) who showed that machine learning had the potential to be used to learn a Reynolds stress closure for RANS models for a few simple flows. (Milani et al., 2018) applied a related approach to scalar flux modelling for film cooling flows. They hypothesized that while a universal RANS Reynolds stress closure might not exist because of the fundamental non-physical assumptions of local models, it could be possible to learn accurate closures for specific classes of flows. The authors therefore focused on film cooling flows and explored the ability of these models to generalize across blowing ratio and hole geometry. Their work showed the potential of these flow-specific models to provide the balance required between predictive accuracy and computational cost in order to enable rapid iteration and design of turbomachinery parts. The heat flux model developed for a jet in crossflow by (Weatheritt et al., 2020) is a good example of application in a CFD environment.

A key challenge in incorporating machine learning closures into the physics-based models is respecting the known physics. Ling et al. (2016a,b) demonstrated that incorporating Galilean invariance directly into the model form can improve the model accuracy in their turbulence closures. Furthermore, they showed that if this invariance is not incorporated into the model directly, it can take much more data for the model to learn the invariance, and even then, it is not perfectly respected. A critical step in developing these data-driven closures is therefore to assess the known physics constraints upfront and build these into the machine learning models by design.

A related challenge is model interpretability. It is unsatisfying to build a machine learning model that is more accurate than a conventional turbulence closure without any insight into how the data-driven model is making its predictions. It is important that as we develop these data-driven models, we also develop approaches for interpretability. (Wu et al., 2017) showed how the t-SNE visualization approach could be used to assess generalization and extrapolation in their data-driven turbulence models. By visualizing the degree of overlap in the projected t-SNE space, they could assess the extent to which their trained machine learning model would be extrapolating on a new flow, and therefore whether or not to have confidence in the model predictions on the new flow. Because turbomachinery design often involves many simulations of related flows, it is important to use visualization and interpretability approaches such as t-SNE to understand when data-driven models are extrapolating and when they can be used with confidence.

Milani et al. (2020) adapted the t-SNE approach to film cooling flows, using this visualization approach to assess the generalization of his scalar flux closure model to new film cooling geometries and blowing ratios. They also investigated the use of spatially-varying feature importance metrics to shed light on which closure terms were important in which regions of the flow. Further development of such interpretability techniques will be of increasing importance as the role of data-driven methods in scientific and engineering applications like turbomachinery grows.

Data management

This paper has surveyed some of the key opportunities for AI to be impactful in the development of the next generation of gas turbine engines and turbomachines in general. However, one of the critical underlying challenges is in data management. For AI to be successful, the data need to be available. As data are also key to a successful design it is desirable to describe how a design proceeds from the conceptual to the validation phase.

Virtual testing – Virtual testing data base (VT)

LES and DNS of a full real engine are still practically impossible, and it is equally impossible to run a large number of design iterations. Still LES does offer the opportunity to retire design risk with a small number of component or sub-system simulations, as done by (Meloni et al., 2019) who ran LES to verify the insurgence of combustion dynamics in a heavy-duty combustor, and by (Andreini et al., 2017) who investigated hot streaks in combustor-turbine interaction. High-fidelity simulations have also been used to identify performance top offenders and the relative design parameters to concentrate on, as discussed by (Legani et al., 2019) who analysed an LPT stator-rotor interaction LES with the aid of POD. With LES, or DNS when possible, performed at realistic operating conditions and with enough geometry details the simulations are accurate enough to represent a sort of “virtual test” the accuracy and resolution of which is superior to experimental test.

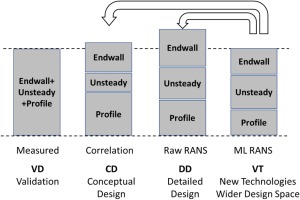
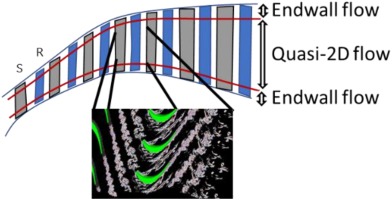
Figure 8 summarizes the challenges associated to the different data sets when applied to the prediction of turbine performance. In Figure 9 losses are generally split into profile and endwall, while losses generated by the unsteady stator-rotor interaction are lumped together with profile losses, partly because measurements have large difficulties to accurately resolve the unsteady flow field. The split between profile and endwall losses is somewhat arbitrary, as demonstrated by (Marconcini et al., 2019), who used both LES and RANS to dissect the spanwise loss generation mechanism in a legacy low-pressure turbine. The relative importance of profile and endwall losses is of paramount importance to blend the spanwise airfoil load. (Michelassi et al., 2015; Michelassi et al., 2016) used both DNS and LES to investigate how unsteady stator-rotor interaction losses evolve and concluded that conventional design correlations as well as RANS are not equipped to account for this extra entropy source, so that the loss split predicted by correlations in the conceptual design phase may be partly inaccurate (see Figure 8). Therefore Figure 8 suggests a fourth pillar, called “virtual testing”, that should be conducted by running high-fidelity CFD to investigate new design spaces or shed light into specific flow mechanisms, in this case the correct split between the different loss sources. Ideally VT should not only help RANS, but also conceptual design correlations to let the designer take accurate decisions early on in the design process.

Figure 8.

Schematic of the design process applied to gas turbines.

Figure 9.

Sketch of a low-pressure turbine.

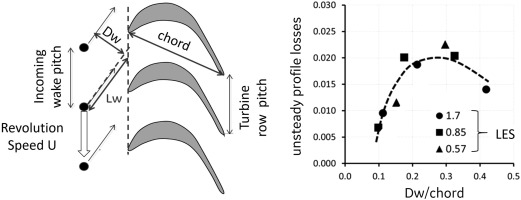
An example of the opportunities and challenges offered by the use of VT data and their potential impact on design rules by providing data to improve CD correlations is given by (Michelassi et al., 2016), who ran several LES to determine the effect of two key design parameters, the flow coefficient defined as

φ=(axialspeed/revolutionspeed),

and the reduced frequency defined as

FRed=(incomingwakespassingfrequency)×(airfoilaxial chord)airfoilexitvelocity

on low pressure turbine losses. The simulations revealed how the concerted impact of these two parameters govern the extra losses generation caused by the unsteady interaction between the turbine row under investigation and the wakes generated by upstream airfoil row. φ and FRed concurrently define the incoming wake dynamics, and in particular, the normal distance of incoming wakes labelled Dw in Figure 10. Dw correlates very well with the predicted unsteady loss contribution as visible in Figure 10, right. While design correlations based on conventional CD data may account for the impact of φ on losses, they never account for the combination of φ and FRed that must be included to further improve the conceptual design correlation accuracy.

Figure 10.

Left - Incoming wakes impinging on a low-pressure airfoil. Right – Unsteady losses as a function of Dw for different combinations of φ and FRed. Adapted from (Michelassi et al., 2016).

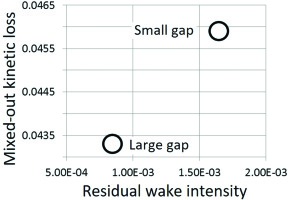
Pichler et al. (2018) investigated the impact of the axial distance between stator and rotor rows on losses. Simple CD design correlations suggest that turbine performance deteriorates when the stator rotor distance increases because of the increase in the endwall wetted surface. Still the LES by Pichler revealed a more complex mechanism happening away from the walls according to which an axial gap increase could actually improve performance by letting the incoming wake decay more thereby reducing the downstream rotor unsteady losses, as illustrated in Figure 11. The LES database also suggested a simple parameter to weigh the residual stator wake intensity at the rotor leading edge (Pichler et al., 2018).

Figure 11.

Rotor losses variation with upstream stator axial distance, adapted from (Pichler et al., 2018).

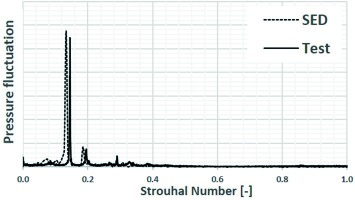
Similarly (Meloni et al., 2019), took advantage of the superior accuracy of LES to predict the onset of combustion dynamics in an annular combustor of a light-industrial gas turbine. The accuracy of the pressure fluctuation is important to determine the severity of the instability, as well as the fluctuation frequency is instrumental to accurate sizing of appropriate acoustic dampers that guarantee a stable combustion regime across a wide operating range. In Figure 12 the comparison between measured and predicted frequency of the pressure fluctuation shows a fairly good match that, despite a small frequency shift, is enough to drive a safe combustion system design.

Figure 12.

Self-Excited-Dynamic (SED) predictions of non-dimensional frequency in terms of Strouhal number and pressure fluctuation amplitude, p’, adapted from (Meloni et al., 2019).

To summarize, in these examples the capability of VT data to resolve physics allowed to determine the underlying fluid flow mechanisms and ultimately suggest not only better designs, but also better early conceptual design correlations and hints to further improve performance. The reconciliation of all the large and heterogenous data sets described above, CD, DD, VT, VD, is challenging due to the large number of data with variable degree of accuracy and resolution in space and time and relevant to different operating conditions. Nevertheless, this is of paramount importance to refine the accuracy of design tools by improving models and modelling assumptions and ensure consistency across conceptual through detailed design, validation and asset field operation phases, as described by (Michelassi et al., 2018). Data management plays a fundamental role here to make sure that relevant data are readily available to extract valuable engineering information.

While it is possible to proceed with smaller data sets by incorporating physical constraints and scientific domain knowledge, it is still important to have the available data structured and digitized in a consistent format. Furthermore, the data need to be accessible across an R&D organization, not silo-ed on an individual's workstation. Beyond access, the data also must be contextualized so that other members in the engineering organization can understand how the data were generated. Without this context, a responsible engineer would not have the confidence to reuse the data structured by a colleague to train machine learning models. While artificial intelligence generates much of the excitement and a large number of scientific papers, data management is the foundation upon which it rests.

The data management requirements for machine learning applications differ from those of conventional laboratory information management systems (LIMS). The goal for data management in this case is not to look up specific experiments for IP or legal protection, but rather to aggregate data across multiple projects and engineers. Therefore, consistency in naming conventions, flexibility in data structure, and the ability to link and compare disparate data sources are all top priorities when managing data for machine learning use cases.

In the context of the various sources of information listed above (CD, DD, VT, VD), it is also critical that the data from these sources be linked appropriately so that analysis and machine learning models can use these data in combination. For example, it would be important that LES and RANS simulations of the same flows would be labelled and linked to enable direct comparison of these simulations, for example as training data inputs and outputs as in (Ling et al., 2016a,b) . In order to compare engine test data with component-level data and simulation data of specific sections of the engine, it is critical that each of these data sources be tagged with the appropriate metadata for future researchers to analyse discrepancies and trends. Any organization interested in building AI capabilities should first assess its current data management practices and include a plan for data management investments in its digital initiative.

Conclusions

Machine learning has the potential to have a transformative impact in powering innovation in the turbomachinery industry. This paper has highlighted three potential avenues for this impact. First, driving accelerated development of high-performance materials using sequential learning for experimental design. Second, enabling co-optimization of materials and part performance for higher performance parts with reduced materials development risk. Third, replacing traditional physics model closures with data-driven closures that respect the physical constraints and invariants and are tuned to specific classes of flows.

A common thread between these three opportunities is the combination of both data-driven methods and traditional scientific methods. None of these approaches replace scientific expertise with a black box AI model: all of them use the scientist domain knowledge as the foundation upon which data-driven methods build. While conventional AI application areas such as e-commerce and ad targeting technology might rely on big data to train AI models without expert knowledge, the case is different in turbomachinery because of the lack of traditional big data sources. Data tend to be more limited (e.g. hundreds or thousands of data on different materials) or highly sample biased (e.g. different production runs of the same material or different points in the same LES simulation). With this limitation on available independent data, the integration of scientific expertise and theory becomes critical so that the machine learning model is building on that foundation rather than re-learning the basics.

In line with this overarching philosophy of combining scientific expertise with data driven models, this paper also highlighted two areas for further research: approaches for integrating domain knowledge into machine learning models and techniques for interpreting the predictions of machine learning models to assist the designer from the early conceptual until the final detailed design phases. The ultimate goal is to reduce the number of design iterations, reduce the design uncertainty and consequently reduce design margins where not strictly necessary, and help the exploration of new design spaces.