Introduction

Aircraft and engine manufacturers as well as policymakers need to focus on the economic and the environmental impact of air traffic, due to the expected strong growth in air traffic, in order to reach the specific objectives of the Advisory Council for Aeronautics Research in Europe (Kallas and Geoghegan-Quinn, 2011). Hence the aim in the development of new aircraft engines is to improve the overall engine efficiency e.g. by increasing the engine bypass ratio. Certain constraints must be observed here, e.g. cruise drag, which is directly coupled to the nacelle diameter, aerodynamic and aeroacoustic factors, which limits the maximum tip speed. A promising concept of such a high bypass ratio engine is the Geared Turbofan (GTF) with a bypass ratio of up to 18. With this technology fuel consumption and noise emissions can be reduced drastically (Riegler and Bichlmaier, 2007).

The side effect of increasing the bypass ratio and thus decreasing the fan pressure ratio is that the fan system becomes more susceptible to perturbations of the incoming flow. A consequence could be the stalling of the fan, which would make a safe operation of the engine impossible. For this reason the interaction between the performance of the fan and the intake flow, especially under off-design conditions, is of major interest. A typical off-design condition is the occurrence of crosswind, especially in the starting phase of an air plane. Several experimental and numerical investigations deal with either fan aerodynamics or nacelle aerodynamics. Only few studies are concerned with the interaction of both. Therefore the objective of the PTF is to provide a combined research setup, including both: wind tunnel capabilities and an operating fan rig. As a result, the fan system can be tested in combination with a representative intake geometry at most critical operation points that occur during flight (Krone and Friedrichs, 2014). An essential question here is whether it would be possible to reproduce an intake separation pattern and thus to generate representative flow for the downstream fan stage in atmospheric wind tunnels. Given that this facility represents an innovative concept, an extensive validation process, both numerical and experimental, is necessary to show the comparability of wind tunnel experiments and experiments under real flight conditions. As a first step the validation process was carried out using the LARA-intake. It has been developed within the work on Hybrid Laminar Flow technology (HLF) in cooperation by Rolls-Royce, Snecma, Hispano-Suiza, ONERA and the DLR (Lecordix, 1996) and has already been investigated by ONERA (Raynal, 1994) in detail providing a well-suited database for experimental validation of the test facility. Furthermore, the LARA-intake is still subject to several numerical and experimental studies with regard to distorted intake flow of the nacelle and fan. (Colin et al., 2007a) conducted extensive numerical research on the LARA-intake under pure crosswind flow. Their research included the ability of different RANS models to predict the correct flow behaviour of the intake flow under crosswind conditions, which is mainly driven by the correct prediction of the flow separation and reattachment process of the boundary layer. The authors also showed the necessity of using a transition model which incorporates laminar boundary layers and its transition to turbulent flow. (Hall and Hynes, 2006) investigated a hysteresis phenomenon with a scaled model of a fan and intake under crosswind conditions. Such a hysteresis of the separated flow region is achieved by running a series of tests with decreasing crosswind angles followed by increasing the crosswind angle again in combination with increasing the mass flow rate through the nacelle with the starting point being a separated intake flow or decreasing the mass flow rate with the starting point being an attached intake flow. Thereby, differing flow patterns for the same operating point develop. Several influences on the hysteresis region and thus the intake flow was examined. Amongst others the influence of the Reynolds number, stream-tube contraction ratio and ground clearance were analysed. It was shown, that while increasing the crosswind angle, the flow separates at a much larger value of the crosswind angle α than for the reattachment while decreasing the crosswind angle. Since the Reynolds number seems to have a considerable effect on the intake flow, some past work was dedicated to its effects on intake performance. For example, (Younghans et al., 1982) showed, that an increased Reynolds number leads to a greater resistance to flow separation and overall lower losses.

As a first step a validated numerical setup has been generated using discrete measuring points of the PTF LARA campaign as well as the pressurized ONERA data set. In a second step the Reynolds number effect has been pointed out via the distortion coefficient of the fan face as well as the isentropic Mach number at the lip. Furthermore, the sensitivity of the crosswind angle and Reynolds number on the numerical predictability of the experimental validation results as well as the observed separation hysteresis will be shown and discussed in detail. Following this a detailed analysis of the discovered hysteresis effect has been done. So far, neither an established theoretical basis for analysing the aerodynamic behaviour of the separation hysteresis nor the ability of the RANS turbulence and transition models exists. This leads to further numerical and experimental investigations in this paper on the aspirated LARA-intake under pure crosswind conditions to give deeper insight to the aerodynamic behaviour of a separated intake under crosswind conditions.

Experimental setup

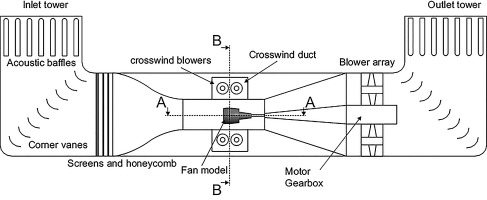
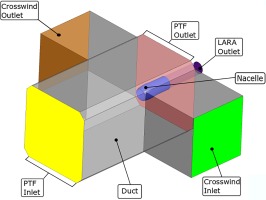
The facility layout of the PTF represents an atmospheric wind tunnel (Eiffel-configuration). As seen in Figure 1, the flow is sucked in via the inlet tower and is redirected by the corner vanes. Screens and a honeycomb improve the flow quality before it enters the test section, where the test vehicle is located. In total eight blowers are generating a maximum headspeed corresponding to Ma0=0.20. They are located behind the diffusor together with the main drive motor, which drives the fan of the test vehicle via an 8 m long shaft. Downstream of the blowers, corner vanes lead the flow towards the outlet tower.

Figure 1.

Experimental setup of the PTF.

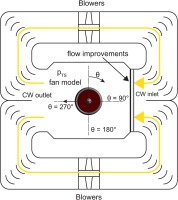
In order to induce an angle of attack to the flow or create pure crosswind conditions, the test section is surrounded by a circumferential crosswind duct. At the crosswind outlet the flow is divided. As seen in Figure 2, half of the mass flow is guided above and the other half below the test section. The whole crosswind duct is powered by four blowers in total. At the crosswind inlet the streams are merged together before the flow is smoothened by screens and honeycombs. The test vehicle itself is not pitchable.

Figure 2.

Circumferential crosswind duct — section B-B.

To generate an intake distortion, the incoming crosswind creates a blocking effect which deflects the main flow. As a result, the test section headwind has an angle of attack with respect to the fan model's rotation axis during crosswind operation. To preserve flow quality, the crosswind mass flow itself and the shear layer are not entering the intake model (Krone and Friedrichs, 2014). By changing the ratio between the headwind and crosswind mass flow, the angle of attack can be varied continuously without any steps.

The Aspirated-Intake-Rig (ASI-Rig) has been designed to test aspirated intakes without a main flow component (Krone et al., 2019). As a consequence of the atmospheric conditions, the flow through the nacelle needs to be generated by an aspirating fan using the power of the main shaft. This fan is located further downstream to prevent interaction with the nacelle flow. The distortion at the fan face of the LARA nacelle is measured by using a measuring section. Six long and six short rakes are located circumferentially around the hub cone. To resolve boundary layer effects, the distance between the total pressure probes towards the wall is shortened.

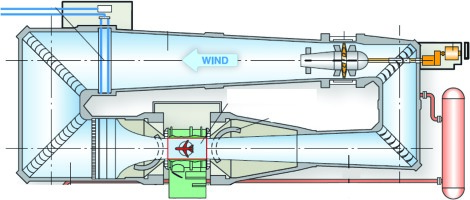
Compared to the PTF wind tunnel, the ONERA F1 wind tunnel, in Le Fauga, is a closed loop, pressurized wind tunnel that can operate up to an ambient pressure of 3.85 bar, it is capable of independently varying the Mach and Reynolds numbers, in order to operate at realistic flight conditions. In contrast to the PTF the F1 tunnel has just one main blower. Therefore, the incoming flow angle can only be set geometrically by pitching the whole nacelle in the test section. For through-flow nacelle tests, the static pressure gradient between the test section and ambient is used to drive the flow through the nacelle to the outside environment. Figure 3 shows the cross section of the tunnel.

Figure 3.

ONERA F1 windtunnel in Le Fauga.

Evaluation planes

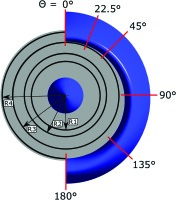
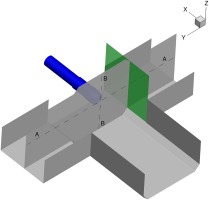
The evaluation planes are shown in Figure 4 and cover the windward side of the nacelle and the fan plane. Along the nacelle contour the surface pressure is evaluated at six different sections. The total pressures on the fan face were evaluated along four different radii, ranging from 50% to 98% of the radius the fan face.

Figure 4.

Evaluation planes of the LARA nacelle.

The results were plotted using the following parameters. The pressure distributions were evaluated by using the isentropic Mach number Mais which is defined as follows:

Mais=2γ−1⋅pt,ambps,local(γ−1)/γ−1

A parameter to analyse the intake distortions of the fan face is the Distortion Coefficient DC60.

DC60=p¯t2−p¯t2,60q¯2

In this equation p¯t2 is the area averaged total pressure of the fan face plane. p¯t2,60 is the area averaged total pressure of a 60°-segment around a certain circumferential angle ϴ. This difference is normalized by the area averaged dynamic pressure of the fan face plane q¯2.

ξ=pt,localp¯t2

Additionally, the total pressure distribution on the fan face plane is evaluated along the radii shown in Figure 4. The considered parameter is ξ which is the ratio of the local total pressure to the averaged total pressure on the fan face plane.

Numerical setup

The experimental results of both the through-flow setups of PTF and ONERA, are used to establish a suitable numerical setup for validation purpose and to investigate the capability of conventional RANS turbulence and transition models to predict such kind of flows accurately.

The simulation domain is shown in Figure 5. This domain contains the test section with the LARA nacelle, the outlet is extended by approximately 5⋅D2 downstream to ensure numerical robustness at stalled intake conditions. Some simplifications are done, e.g. no modelling of the instrumentation in the fan face plane or the support structure.

Figure 5.

Numerical Setup.

In the experimental setup the crosswind condition is realized by the facility's crosswind tunnel. Therefore, the crosswind enters the numerical domain through the crosswind inlet boundary condition (green) and leaves the domain from the opposite side, through the crosswind outlet boundary condition (brown). Since the facility's crosswind tunnel forms a closed loop, the crosswind mass flows that enter and leave the domain are equal. The test section inlet (yellow) is defined as a velocity inlet to take the ejector effect into consideration and ensure numerical stability. The test section outlet (red) is defined as a pressure outlet boundary condition. To reach the desired Mach numbers at the fan face plane, the intake outlet (purple) is defined as a pressure outlet boundary condition. In order to investigate different Reynolds numbers, the density of air inside the domain had to be varied by changing pressure to 1 bar (representative for the PTF experiments), 2.5 bar and 3.85 bar (representative for the ONERA experiments). The Reynolds number is defined as

with D1=0.3595m which is the diameter of the highlight plane of the LARA nacelle. Accordingly, the pressure at the LARA outlet boundary must be set to attain the desired Mach number in the fan face. Matching conditions were assured by monitoring the Mach number at the fan face.

Computational grids of an increasing number of cells were generated using the commercial grid generator ICEM-CFD of ANSYS. The sensitivity analysis conducted by (Kellersmann et al., 2013) for the same set up, showed that at least 28.8 million cells were required to model the overall performance parameters accurately and a y+≈2 was required for proper resolution of the boundary layers. The mesh used for the study is block-structured and features an OH-topology.

Turbulence modelling

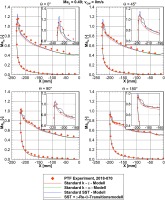
Preliminary simulations were performed using ANSYS CFX with different turbulence models in order to find the best suited numerical setup. Figure 6 shows the static pressure distribution along the nacelle contour on different circumferential positions ϴ (cf. Figure 4) for various turbulence models compared to experimental data. The drawbacks of the k-ε for predicting aerodynamic flows with adverse pressure gradients are well known and show up in these results. The results for the k-ω and SST model seem to slightly over predict the suction peaks for every circumferential position ϴ. The transition modelling (γ−Reθ) with the SST model agrees best with the experimental results. A laminar separation bubble can be observed in the numerical results. The transition process seems to have an important influence on the intake flow. This was observed by (Colin et al., 2007b). Therefore, the apt turbulence model for the following investigations was chosen to be the SST model with additional transition modelling by the γ−Reθ transition model by Menter and Langtry (Menter et al., 2006).

Figure 6.

Isentropic Mach number distribution for various turbulence models and the magnifications of the suction peaks.

Sensitivity to crosswind angle

Another objective of this paper is to assess the sensitivity of the intake flow to the crosswind angle. Therefore, two different crosswind angles were evaluated numerically. The crosswind angle αcw can be changed by varying the velocity at the PTF inlet. This angle is evaluated at the green plane shown in Figure 7. This plane is representative for the crosswind window. Additionally, the plane directly in front of the LARA nacelle shows the slices along which α and β are evaluated.

Figure 7.

Evaluation planes of the flow angles alpha and beta.

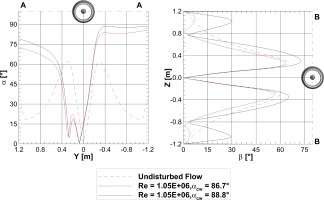
Figure 8 illustrates the flow angles directly in front of the nacelle. α represents the flow angle in the X-Y-Plane and is therefore directly related to the crosswind angle, while β represents the flow angle in the X-Z-Plane.

Figure 8.

Flow angles directly in front of the nacelle.

In Figure 8, three different results are shown. The dashed curve shows the undisturbed flow without crosswind interaction. The remaining two show the angle distributions for two different crosswind angles αcw. In the upper plot of Figure 8, the undisturbed flow exhibits a symmetrical flow pattern with the symmetry plane being at Y=0m. The two maxima at Y≈0.3m and Y≈−0.3m, represent the boundary of the captured stream tube. The minimum at Y=0m with α=0∘ is representative for a flow parallel to the machine axis of the nacelle. The effect of the crosswind is directly seen as a larger value of α on the right side of the nacelle, where the source of the crosswind is located. At the same time the other local maximum shows lower values of α compared to the undisturbed flow. Thus, the two local maxima, which represent the capture stream tube, show a behaviour where their positions are shifted towards the crosswind source. The minimum is shifted to Y=0.08m, in the direction of the crosswind. The values of α approach 90°, again, towards the crosswind outlet.

The lower plot of Figure 8 shows the results for β. The undisturbed flow shows two maxima. One is representative of θ=0∘ at Z=0.25m and the other one is representative of θ=180∘ at Z=−0.32m. The upper maximum shows a larger value of β than the lower one. This is caused by the contour of the nacelle. The upper lip is thinner and exhibits a higher curvature. Therefore, the turning of the flow is higher around the upper lip than for the lower lip. The crosswind expresses itself by a shift of the values of the maxima. While the results with αcw=86.7∘ show reduced values compared to the undisturbed flow, the results with αcw=88.8∘ show higher values. This directly affects the static pressure distribution along the nacelle contour, shown in Figure 9.

Figure 9.

Isentropic Mach number distribution for different crosswindangle α_cw.

This illustrates the experimental data from ONERA and the two numerical results with the same crosswind angles as discussed above. The static pressure distribution is sensitive to the turning of the flow around the nacelle. The higher the crosswind angle the stronger the suction peak. This is best shown for θ=90∘ which indicates the highest degree of dependence, since it is directed straight to the crosswind flow. A change of Δαcw=2∘ shows a considerable influence on the intake flow. The reason for the higher peak Mach numbers is the position of the stagnation point on the outer nacelle contour. The greater the crosswind angle, the further downstream the stagnation point. This results in higher flow acceleration and thus a higher velocity. Since the simulation needs a velocity specified at the PTF Inlet it is not possible to reach a crosswind angle of αcw=90∘. In order to approach αcw=90∘ as close as possible the velocity at the PTF inlet was kept as low as possible while still maintaining a stable simulation.

Additionally, the results show that the experimental data acquired by ONERA can be reproduced with the numerical setup used in this paper. However it is noted, that the crosswind velocity was set to vcw=15.4m/s in order to match the ONERA experiments. The PTF experiments and simulations were done with vcw=11.3m/s. This means the experiments done by ONERA can not be directly compared to the PTF experiments. Figure 9 indicates that the experimental data by ONERA with a higher Reynolds number can be numerically reproduced. Therefore, the sensitivity to the Reynolds number will be discussed with respect to the numerical results.

Results and discussion

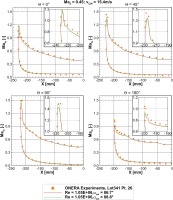
The first results of the LARA campaign at the PTF has shown that the pressure distribution at the lip seems to have a general sensitivity towards the Reynolds number (published in (Krone et al., 2019)) especially for the pressure distribution at θ=90∘. The following section will address the scientific understanding and complement it by further numerical investigations.

Reynolds number

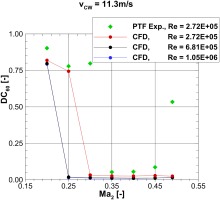
The sensitivity towards the Reynolds number for intake flows under crosswind conditions is shown in Figure 10, where the Distortion Coefficient DC60 is plotted against the fan face Mach number, Ma2 across the operating range of the intake, for three different Reynolds numbers, of which the lowest represents the PTF experiments at ambient conditions. Ma2 is defined as the averaged Mach number at the fan face without crosswind calculated by the average dynamic pressure:

Figure 10.

Distortion levels for different Ma₂ and Re-numbers at 11.3 m/s crosswind.

Ma2=2⋅q¯2ργRsT2

The rising Reynolds number shows its effect on overall reduced distortion levels. Additionally, higher the Reynolds number, higher the flow's resistance to separation onset. This can be seen in Figure 10 at Ma2=0.25. While the high value of the DC60 for the lowest Reynolds number indicates a separated flow, the low distortion levels for the two higher Reynolds numbers indicate an attached intake flow.

Younghans et al. (1982) explained the decrease of boundary layer thickness with an increasing Reynolds number. A thinner boundary layer can better withstand a given adverse pressure gradient, thus delaying the separation onset to a lower Ma2. By taking a look at ξ (see Figure 11) the Reynolds number effect on the boundary layer size can be identified.

Figure 11.

Total pressure distribution along different radiuses for different Reynolds numbers at Ma₂ = 0.45.

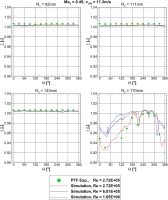
R₁ to R₃ are representative for the core flow. The values greater than one can be explained by the influence of the boundary layer. The total pressure losses in the boundary layer reduce the value of the averaged total pressure of the fan face. Since the boundary layer thickness decreases with an increasing Reynolds number, ξ results into lower values for rising Reynolds number, because the averaged total pressure in the fan face increases. The boundary layer itself can be seen by ξ at R4. The effect of the crosswind is clearly visible between θ=0∘ and θ=180∘ in the form of reduced total pressures. This effect decreases with rising Reynolds numbers. This results in the overall lower distortion levels at higher Reynolds numbers, as depicted in Figure 10.

Apart from the distortion coefficient the effect of the Reynolds number can be pointed out by the analysis of the static pressure distribution at the lip — as seen by the isentropic Mach number distribution in Figure 12.

Figure 12.

Isentropic Mach number distribution for different Reynolds numbers at Ma₂ = 0.45 and the magnifications of the suction peaks.

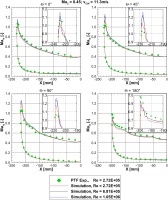
The Reynolds number affects the characteristic of the suction peak for each section ϴ. The higher the Reynolds number the higher the maximum suction peak. This is directly connected to the development of a laminar separation bubble, which can be observed in every subfigure of Figure 12 in the form of a constant pressure plateau followed by a further decrease of isentropic Mach number. This transition process has a substantial effect on the development of the suction peak. With an increasing Reynolds number, the extent of the separated region within the bubble reduces, as seen by the surface streamlines in Figure 13. Thereby, the magnitude of the suction peak increases with the Reynolds number.

Figure 13.

Declining separated region within the separation bubble due to the increasing Reynolds number — seen by the surface streamlines at Ma₂ = 0.45.

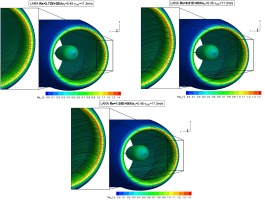
A similar effect was observed by (Jacobs and Sherman, 1937) and (Pinkerton, 1938) while investigating NACA airfoils. The authors showed that an increasing Reynolds number leads to a reduced transition region where the turbulent reattachment point moves closer to the laminar separation point, thus reducing the extent of the separated region. This result in a higher suction peak and lift coefficient.

Hysteresis effect

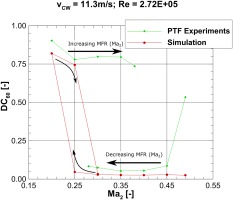
During the experiments at the PTF a separation hysteresis was encountered. Figure 14 shows the hysteresis for the low speed separation by plotting the DC60 against the fan face Mach number, Ma2, across the operating range of the intake. In the experiments the hysteresis is achieved by either increasing the mass flow rate through the nacelle while starting from a separated intake flow or decreasing the mass flow rate while starting from an attached intake flow. Thereby, differing results for the same operating point Ma2 develop.

Figure 14.

Hysteresis effect shown by plotting the DC₆₀ over Ma₂.

This can be partly reproduced with steady state simulations as shown in Figure 14 by using different results as initialization for the simulation. The operating point corresponding to Ma2=0.25 shows two different numerical results, even though identical setup and boundary conditions. In order to achieve a solution with an attached flow the simulation was initialized by using the results of the operating point corresponding to Ma2=0.30. The solution with a separated flow is achieved by initializing the simulation with the results of an operating point where the flow is separated (Ma2=0.20).

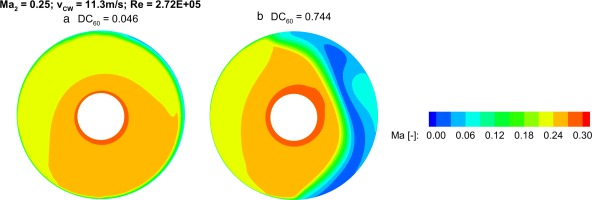
This ambiguity is illustrated in Figure 15 where the Mach number distribution at the fan face plane is shown. The crosswind source in both cases is coming from the θ=90∘ position. Subfigure (A) shows a rather homogenous flow pattern with no visible flow separation, whereas subfigure (B) displays a large separation region on the windward side of the fan face, justifying the high DC60 values.

Figure 15.

Distribution of the fan face Mach number midst hysterese region.

However, the RANS approach is not capable of reproducing the whole hysteresis region. At Ma2=0.30 the two results are independent to the initialization procedure. Both results indicate an attached flow with only a minimal difference in the DC60- whereas the experimental results show an ambiguity to up to Ma2=0.40. This is most likely explained by the well-known drawbacks of the SST model to predict separated flows. (Colin et al., 2007a) came to similar results with an unsteady simulation approach, the hysteresis was partly reproduced but only to a small extent compared to the experimental results.

At present there are no established theoretical bases for analysing aerodynamic hysteresis and it remains a difficult phenomenon to understand. (Hall and Hynes, 2006) have shown in their work, that separation hysteresis is particularly sensitive to independent variation in stream-tube contraction ratio, ground clearance and Reynolds number. Further studies have pointed out that the separation hysteresis also occurs during static stall condition of an airfoil at high angle of attack (Mittal and Saxena, 2000).

Conclusions

This publication deals with the experimental and numerical investigation of jet engine intake distortions caused by crosswind conditions. In the institute's own propulsion test facility (PTF), experimental investigations of the well-known LARA nacelle under pure crosswind conditions were carried out and compared with already existing experimental data of the same test vehicle in the F1 wind tunnel of ONERA in Le Fauga.

A comparison of the experimental results of the LARA nacelle measured within the PTF to the results measured within the F1 wind tunnel of ONERA at same Mach and Reynolds number of the inflow shows a clear difference in the isentropic peak Mach number distribution in the area of the leading edge lip of the nacelle. Additional numerical investigations showed that the isentropic peak Mach number depends on the Reynolds number as well as on the size of the occurring separation bubble. As the Reynolds number increases, the size of the separation bubble decreases, increasing the suction peak. In addition to this, it could also be shown based on the numerical results that the isentropic Mach number distribution is very sensitive to the angle of the crosswind. The larger the crosswind angle, the larger the suction peak. The reason for this is the position of the stagnation point, which moves further downstream by increasing the crosswind angle, resulting in higher flow acceleration around the lip of the nacelle.

Within the scope of these validation tests, a hysteresis effect of the separation and reattachment process of the occurring flow separation was observed in the experimental investigations. This hysteresis effect occurs when the crosswind and the nacelle mass flow are increased and/or decreased to adjust the different operating points. Therefore, different results for the same operating point develop. At present there is no established theoretical basis for the analysis of this aerodynamic hysteresis. Further fundamental detailed investigations on the mechanisms of this effect have to be carried out.

At present and in future studies, high-resolution measurement techniques will be used to investigate this highly three-dimensional and transient phenomenon. In addition, the hysteresis effect has to be investigated numerically in further studies. Current results using conventional steady RANS simulations have shown that the hysteresis effect can only partly be reproduced compared to the experiments. Further studies on this topic will try to achieve an improved numerical prediction of this phenomenon with transient simulations based on Reynolds stress modelling (RSM).

Nomenclature

Competing interests

Lennart Harjes declares that he has no conflict of interest. Christoph Bode declares that he has no conflict of interest. Jonas Grubert declares that he has no conflict of interest. Philip Frantzheld declares that he has no conflict of interest. Patrick Koch declares that he has no conflict of interest. Jens Friedrichs declares that he has no conflict of interest.