Experimental setup

The axial turbine research facility LISA of the Laboratory for Energy Conversion (LEC) at ETH Zürich is a long-duration, moderate-speed, low-temperature rotating facility. It consists of a quasi-closed air loop including a centrifugal compressor, a two-stage heat exchanger, a 3 m-long flow conditioning stretch for flow uniformity upstream of the turbine, the turbine itself and a calibrated Venturi nozzle for mass flow measurements. The flow undergoes an acceleration upstream of the turbine stage, thus reducing further the impact of any non-uniformities left after the conditioning stretch. The heat exchanger controls the turbine inlet total temperature T_t,in to an accuracy of ±0.3 K

A DC generator, coupled to the turbine shaft via a gearbox, acts as break by converting the mechanical power produced by the turbine into electrical power, which is fed back to the grid. The rotational speed is controlled with an accuracy of ±0.02% (±0.5 rpm). A torque meter is installed on the vertical shaft between the turbine and the gearbox. At the exit of the test section, two successive rows of deswirl vanes recover the static pressure before going through the venturi nozzle and back to the compressor. For more details on the rig the reader is referred to 27.

A 1.5 stage, high work turbine configuration is installed in the test section of the facility. Both airfoils and endwalls have a complex 3D geometry optimized for minimizing the aerodynamic losses.

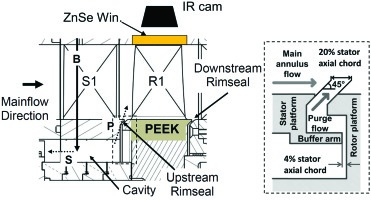
Air is spilled from the main air loop upstream of the flow conditioning stretch and fed to the stator/rotor cavity through the first stator vanes. The amount of by-pass flow “B” (see Figure 1) is measured via a standard nozzle. The purge flow mass flow rate is calculated as the difference between the total by-pass mass flow rate and the secondary leakage flow following the path through the drum, labeled “S” in Figure 1. The injection ratio (IR) is then defined as:

Figure 1.

View from an axial plane of the purge flow path (left). A schematic of the optical setup is included; detail of the stator-rotor rim seal cavity (right).

where m˙S is measured by another standard nozzle. The error on the IR is of ±0.01%. A 45° chamfer on the rotor platform ensures that the purge flow presents an axial component of velocity, relevant for endwall cooling purposes 23. Further details on the purge injection system are found in 24 and 26.

The facility is set up for heat transfer measurements on the rotor by adapting the infrared-based technique used by 17 for stationary parts.

A FLIR SC7300L IR camera records thermograms of the rotor endwall through three IR-transparent ZnSe (Zinc-Selenide) windows mounted on the rotor casing (schematically shown in Figure 1). The camera can be traversed to access more of the inlet portion of the passage.

A controlled thermal boundary condition on the rotor hub endwall surface is achieved by installing a thermally insulating insert (Polyether-ether-ketone or PEEK) in the platform. The insert is instrumented with a film heater deposited on the endwall surface and 9 PT100 RTDs embedded in the substrate, 1.5 mm below the endwall surface, to monitor the conductive heat losses. The heater is obtained by directly depositing a metallic multilayer (10 nm Cr, 200 nm Ni, 10 nm Au) on the CNC-machined PEEK insert by e-beam physical vapour deposition and then by laser cutting the film. A serpentine of uniform width of 1.65 mm is produced with a gap between tracks of 55 μm. High-emissivity paint (ɛ = 0.98) is applied on the whole rotor to allow for accurate temperature measurements and minimize spurious reflections. A correction factor S_q for local heat flux non-uniformities is applied to the nominal value of average heat flux produced by the heater based on the results of step-wise transient heating tests. The electrical heat flux generated by Joule effect is then calculated as:

Where P = i∙V is the electrical power fed to the heater and A is the surface area of the hub endwall. The signal from the PT100 is read out by an on-board data acquisition system sending the readings to a computer via Wi-Fi. The resulting solid temperatures have an error of ±0.5 K.

Power is fed to the data acquisition system and to the heater separately through a two-channel slip ring. The DC power sent to the heater is measured with a voltmeter and an ammeter with an uncertainty of less than ±1.6%.

Measurement procedure

Measurements are performed at steady state for the nominal operating conditions for the rig, summarized in Table 1. The infrared camera records sequences of 1,000 images with two different integration times (10 μs and 50 μs), for two camera positions and four power settings of the heater. In total, each test case comprises of 16,000 images. The acquisition of a frame is triggered once per revolution by the signal coming from an optical tachometer. The two distinct views of the endwall allows for the covering of the inlet portion of the endwall passage until ~80% of its axial extent. Once an infrared camera acquisition is completed, the electrical power fed to the heater is increased to the next level. The average heat flux produced by the endwall heater ranges from 1.4 kW/m² to 8.1 kW/m². The different views of the passage are mapped onto a mesh of the rotor endwall by means of projective geometry as explained by 17. Further details on the geometrical transformation of the images can be found in 10. The long and short exposure data sets are combined after registration and deblurring to produce a high-dynamic range picture of the thermal field. The resolution of the final thermograms is of 0.36 mm/pixels, but due to the movement of the rotor during the integration time, the temperature contours are smeared over 0.97 mm in the circumferential direction.

Feeding current and voltage are constantly monitored, while the solid temperature is recorded in bursts of 5 s during the infrared camera acquisitions.

Calculation of the heat transfer quantities

The calculation of the convective heat flux q"·conv is based on the following energy balance:

Where q"·el is the electrical heat flux produced by Joule heating returned by , q"·cond is the conductive heat loss in the substrate and q"·rad is the radiative heat transfer to the environment evaluated according to:

With ɛ being the emissivity of the surface, σ the Stefan-Boltzmann constant, T_w the wall temperature and T_t,rel the rotor-relative total temperature at the rotor inlet, here taken as a reference temperature for the heat transfer by radiation. The conductive heat loss q"·cond is evaluated based on the readings of the 9 PT100 RTDs and the thermal properties of the substrate according to the following 1D equation:

In , T_w is the wall temperature measured at the normal projection on the endwall of the PT100 location and T_sub is the substrate temperature read by the PT100 thermometer. For each heat flux level, an average value of conductive loss is calculated over the passage and used in the energy balance of . The average values fall between 1.6% and 6.8%.

Finally, the convective heat flux q"·conv is obtained and the heat transfer coefficient h and the adiabatic wall temperature T_aw can be determined. A linear fit is performed through the four data points available for each location on the endwall mesh, being valid the following:

The linear fitting procedure is illustrated in Figure 2.

Figure 2.

Linear fit procedure to calculate heat transfer coefficient h (slope) and adiabatic wall temperature Taw (intercept).

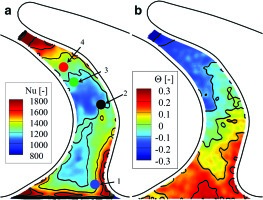
Locations 1–4 are shown in Figure 3.

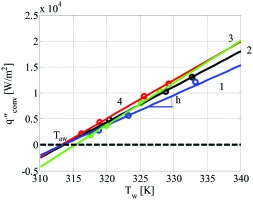
The heat transfer coefficient corresponds to the slope of the lines, while the intercept at q"·conv = 0 is the adiabatic wall temperature. The linearity of the convective heat flux with the wall temperature is highlighted. The locations labelled with numbers 1–4 are marked in the endwall map of Figure 3.

Figure 3.

a) Nusselt number distribution for the reference case, nominal operating condition with no purge flow injection; b) distribution of non-dimensional adiabatic wall temperature .

Computational setup

Transient CFD simulations were performed on a 20° sector of the complete 1.5 stage turbine, including the hub cavity. The mesh was generated in AutoGrid5^TM by Numeca. Approximately 2M cells were used for each passage with an average y⁺ < 1. The simulations were conducted in ANSYS CFX v15.0 with experimental boundary conditions:

The Shear Stress Transport turbulence model and a temporal resolution of 50 time steps per rotor pitch were used. Three complete rotor revolutions ensure a converged aerodynamic flow field with adiabatic walls. An additional revolution was then conducted for each of the two wall heat flux boundary conditions. The results shown are derived from data that was time-averaged over this last revolution.

For comparison, also a steady state result is shown, derived from a mixing plane model. Mesh, boundary conditions and turbulence settings are identical to the transient setup.

Uncertainty analysis

The propagation of the uncertainties to the final results is evaluated by successively perturbing the input parameters of the processing software according to the method described by 20. In particular, the main relative contributions to the mean square error averaged over the passage come from:

The conduction losses q"·cond – evaluated according to and discussed above – are varied between the minimum and maximum values recorded: respectively 0% and 9% of the total local heat flux q"·el.

The correction factor S_q variability is within 3.7% on average over the whole endwall surface, from tests performed in the range 0.9 kW/m² to 2.3 kW/m².

The remaining contributions come from uncertainties on the surface emissivity ɛ = 0.98 ± 2%, electrical power (±1.6%) and relative total temperature at rotor inlet (±1 K).

Effect of purge air on heat transfer quantities

Results are presented for the two injection rate settings of 0.8% and 1.2% referred to the reference case with no purge air injection (0.0%). Particularly, variations in Nusselt number and adiabatic wall temperatures are shown respectively in terms of percentage of the reference Nusselt number (Figure 5) and (Figure 6) and a non-dimensional temperature difference θ (Figure 5) and (Figure 6). The two quantities are defined as:

Figure 6.

a) Comparison between reference case (IR = 0.0%) and IR = 0.8%. Nusselt number relative difference; b) non-dimensional adiabatic wall temperature difference .

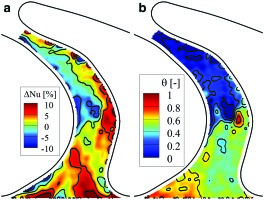
Figure 5.

Experimental uncertainty distributions for non-dimensional adiabatic wall temperature difference.

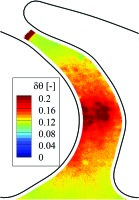
In , T_aw is the local adiabatic wall temperature for the test case of interest, T_aw,0.0% is the adiabatic wall temperature of the reference test case with no purge flow injection, T_t,rel,purge and T_t,rel,MAIN are respectively the rotor-relative total temperatures of the purge flow and of the main flow, obtained by means of probe measurements. Due to the operations in and , the uncertainties in ΔNu and θ are higher than the ones shown in Figure 4. An analytical calculation of uncertainty propagation shows that the uncertainties in ΔNu are ~14% on average over the whole endwall, while the uncertainty in θ is shown in Figure 5.

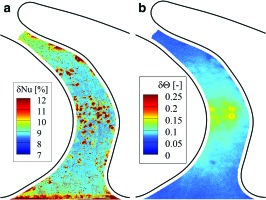
Figure 4.

a) Experimental uncertainty distributions for Nusselt number; b) non-dimensional adiabatic wall temperature.

The definition (9) enables a qualitative assessment of the cooling effect of the purge flow over the endwall. In the current study, density ratios are not representative of cooling conditions in actual engines, being in the order of 1. Furthermore, in this experiment, the cavity flow presents a rotor-relative total temperature higher than the one of the main flow by (2 ± 0.2) K.

Variations of Nusselt number on a point-wise basis are shown in Figure 6 and Figure 7, respectively for IR0.8% and IR1.2%, while laterally averaged profiles of Nusselt numbers are presented for all cases in Figure 8.

Figure 8.

a) Circumferentially averaged Nusselt number for all test cases; b) circumferentially averaged non-dimensional adiabatic wall temperature (see ).

Error bars represent a 95% confidence interval.

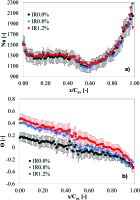
Figure 7.

a) comparison between reference case (IR = 0.0%) and IR = 1.2%. Nusselt number relative difference; b) non-dimensional adiabatic wall temperature difference .

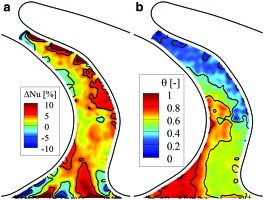
Differences in Nusselt number induced by different rates of purge air injection are generally within the measurement uncertainties both on a local and on a circumferentially averaged basis. Nonetheless, at the very inlet of the passage, close to the suction side of the rotor blade, pairs of islands presenting increases up to 20% of the reference case and decreases of the order of 5% are consistently observed in both Nusselt number distributions recorded for IR0.8% and IR1.2%. The patterns suggest a strengthening of the suction side leg of the horseshoe vortex producing an increase of heat transfer due to the downwash acceleration and a milder decrease corresponding to the upwash acceleration. Similar effects have been observed in turbulent boundary layers perturbed by longitudinal vortices 09. Moreover, increases up to 20% are also recorded closer to the pressure side of the blade and affecting a wider area spanning towards the suction side. This can be related to the strengthening of the passage vortex due to the entrainment of purge flow. Additionally, it is worth noting that the area of Nusselt number increase in the proximity of the pressure side of the blade has a lesser axial extent in the IR1.2% case. This suggests an earlier lift-off of the passage vortex due to the higher radial momentum of the purge flow.

The adiabatic wall temperature distributions underline for both cases (Figure 6) and (Figure 7) how the purge flow is most effective as coolant in the proximity of the suction side of the rotor blade, as expected. In this location, the effect of purge air manifests itself as a local increase of the adiabatic wall temperature. Respectively, the increase is of 0.67 times the difference between the rotor-relative total temperatures of the cavity flow and the main flow for an IR0.8% and of 0.82 times for an IR1.2%.

The local character of the adiabatic wall temperature variation highlights how the purge air has a potential application as coolant for specific rotor endwall locations (i.e., inlet of the passage towards the suction side of the blade).

On a circumferentially averaged basis, Figure 8 shows negligible impact of the purge air injection, while differences are still well distinguishable in Figure 8, especially towards the inlet and until ~30% of the rotor blade axial chord C_ax.

Comparison with numerical predictions

Both predictions and experimental data for IR0.8% show the following features consistently:

Notice that the start of the boundary layer is not present in the CFD results, because the uniform heat flux boundary condition is imposed from further upstream (2% of C_ax) in the model, compared to the start of the heated platform used in the experiments. This was necessary to overcome difficulties in meshing the cavity/main flow path interface.

The general underestimation of the heat transfer level is attributed to the effect of wall roughness, not properly captured by the simulations. An estimation of the non-dimensional sandgrain roughness

can be given based on the measured sandgrain roughness k_s, the mass-averaged relative velocities w measured by probes, Fanning’s friction factor f as calculated by 05 and the kinematic viscosity of air ν at the mass-averaged static conditions measured at inlet and outlet of the rotor. The values are k_s⁺~28 at the inlet of the passage and k_s⁺~47 at the outlet and fall – according to the classification of 21 –, in the transitionally rough regime (5 < k_s⁺ < 70). The doubling of k_s⁺ across the passage can explain, in particular, the divergence of the two corresponding laterally averaged Nusselt number curves in Figure 10.

Figure 10.

Circumferentially averaged Nusselt number profiles.

Shaded area represents experimental uncertainty.

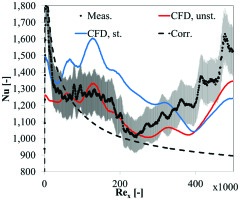
The circumferentially averaged Nusselt number profiles of Figure 10 show good agreement between the experimental data and the unsteady simulations until about 50% of the axial extent of the passage. From this point on, the flow acceleration becomes of relevance and the increase in heat transfer due to the thinner boundary layer is underpredicted. The discrepancy is attributed to a not captured wall roughness effect. The steady CFD simulation tends to overpredict the heat transfer significantly (20–30%). The comparison is completed with a flat plate correlation for turbulent boundary layers on surfaces with uniform heat flux:

The correlation matches the experiments in the initial part of the passage (until ~15–20% of its axial extent), until secondary flows and flow acceleration occur.