Loss analysis

The most accurate and robust method to quantify loss is the assessment of the total amount of entropy present in a thermodynamic system.

Since the system considered is modeled using adiabatic wall boundaries, entropy as per

lends itself as the base quantifier of flow losses. In order to distinguish the losses according to their generating flow phenomena, distinct quantities for identification are needed. The distinction between different sources of entropy is based purely on phenomenological criteria and not on physical entropy-generating mechanisms, i.e., the losses are distributed amongst profile boundary layers, wakes, end-wall boundary layers (hub and tip), and secondary flow.

A common feature which all these flow phenomena share, is that they exist in flow regions where the vorticity ω→=∇→×c→ does not equal zero. The first distinction can be made between secondary flow and boundary layers as well as wakes. Secondary flow consists of vortex structures which can be characterized by their streamwise vorticity

which is the projection of the vorticity vector onto the local velocity vector. Using the Pythagorean Theorem, the vorticity vector can be decomposed into a streamwise and a crosswise component perpendicular to the local flow direction

The crosswise vorticity is characteristic for boundary layers, wakes, and rotational shear layers in general. Based upon these considerations, the following blending factors can be formulated:

and

The subdivision between boundary layers on the end wall or profile and wakes, however, necessitates additional blending factors. To discriminate between end-wall and profile boundary layers or wakes, the vorticity in cylindrical coordinates ω→=(ωx,ωr,ωθ)T is used and the following differentiation between cases is defined:

Here, ψr(ω→) represents a Boolean function, which is “true” or unity, when the local vorticity vector is of predominantly radial orientation, i.e., in the profile boundary layers and wakes. The entropy due to crosswise vorticity of radial orientation is

and

for a deviating orientation of the vorticity vector.

To further isolate the profile boundary layers from the wakes, a distinction is made, based upon the distance normal to the profile dP:

The critical distance of δmax=0.6mm is chosen, which is the maximum boundary layer thickness across all blades of the present configuration.

Regions, where ψr(ω→) returns “false” or zero are consequently characterized by predominantly axial-circumferential vorticity. This is the case in the end-wall boundary layers. But also in some parts of the wakes, as they interact with secondary flow and experience twisting amongst the longitudinal axis of the secondary-flow vortices. The separation between hub and tip boundary layer and the part due to wakes is defined by the relative radial height (r−rmin)/H:

and

The regions between (r−rmin)/H=0.15 and (r−rmin)/H=0.90 are included in the wake losses.

The individual contributions to the overall entropy are, therefore, defined as follows:

The contribution of the secondary flow is given by

the profile boundary layer by

the hub boundary layer by

the tip boundary layer by

and the contribution of the wakes is determined by

Each individual loss contribution is then integrated over the main flow domain, i.e., the turbine excluding the cavities, to obtain the resulting total,

The approach shown here is also used to assess the loss contribution of shock-wave vortex interaction in Mimic et al. (2019) where it is found to produce similarly satisfactory results.

Turbine configuration

The turbine is a low-pressure turbine with an aspect ratio of AR=2.15 as described by Henke et al. (2016). Both stator rows can be moved in axial direction as well as be circumferentially clocked independently from each other, see Henke et al. (2012). Three different axial gaps were chosen for experimental investigation. The gap sizes X are equal to 20%, 50% and 80% of the stator axial chord, respectively. Axial spacings are adjusted in unison for both the stator-rotor and rotor-stator gap. The clocking is adjusted together with the axial-gap variation by changing the circumferential positions of the stator-blade rows relative to each other. This yields a similar incoming wake distribution relative to the blades and enables the isolation of the axial-gap size effect: An imaginary particle originating from the stator 1 trailing edge impinges upon the stator 2 leading edge for all configurations. As the blade count of stator 2 is double that of stator 1 (Tab. 1), only every second blade of the stator 2 passage is directly affected by the stator 1 wake flow.

Detailed aerodynamic characteristics and a base verification of the overall time-averaged flow field can also be found in Henke et al. (2016).

Instrumentation

The instrumentation of the experimental setup has been devised in order to answer the questions posed in the introduction of this paper in terms of time-accurate and time-averaged measurements of the local flow conditions.

To quantify the overall efficiency, rake probes measuring total pressure and total temperature at the inlet and outlet as well as pressure instrumentation on the blade surfaces were designed during a numerical pre-test analysis, including a local optimization of measurement positions.

Figure 1 shows a sectional view of the flow path including the measurement planes (MP). MP00, which is located further upstream of the control volume and thus not shown here, features equally spaced rake probes to verify the homogeneous, swirl free inlet flow of the turbine on a grid of six circumferential rakes with six radial positions each. Rake probes in MP32 have been designed to deliver a 360 deg record of total quantities as well as the static pressure and swirl angle. In order to operate these rakes in the three-dimensional flow field downstream of stator 2, the kiel-head probes have been designed with a pre-twist in order to record accurate data of the local flow-field for all radial measurement positions.

Figure 1.

Schematic of the 1.5-stage turbine test rig. Small gap X/Cax=20% in light gray; large gap X/Cax=80% in dark gray.

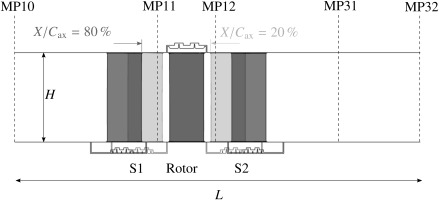
As these rake probes provide only limited radial resolution of the flow field, additional five-hole-probe measurements have been conducted in the measurement planes MP10 (inlet section) and MP31 (outlet section). While rake probes allow continuous data acquisition, probe traverses provide better resolution in radial direction for a specific point in time. A combination of these data sources provides a set of high-resolution boundary conditions for each experiment, which are used in the present work. Within the stator-rotor and rotor-stator gap regions between the blade rows, time-averaged as well as time-resolved multi-hole-probe traverses were conducted for the medium and large axial-gap configuration. For the smallest gap investigated, the remaining gap between two blade rows is too small for probe measurements. Therefore, the blading itself has been equipped with pressure taps (time-averaged and time-accurate wall taps) on the suction and pressure sides and in the leading and trailing edges. This allows determining the wake-flow properties and unsteady flow characteristics for all three axial-gap configurations.

Numerical setup

The experimental data is supplemented by steady and unsteady RANS calculations for all three gaps using the TRACE solver, which is being developed by the German Aerospace Center (DLR) in cooperation with MTU Aero Engines AG. The general numerical setup used in this work is mostly identical to the ones described by Henke et al. (2016) and Biester et al. (2012). The following short summary will focus on modifications to the referenced setups.

For steady-state calculations, mixing planes are positioned at 50% of the axial gap. For unsteady simulations, one blade passing period (BPP) is resolved by 192 time steps; each time step is resolved using 30 sub-iterations. A Courant-Friedrichs-Levy (CFL)-number of 50 is used for all calculations. As a result of the blade counts detailed in Tab. 1, a periodic 60 deg segment is used for the simulations. The k-ω-model by Wilcox (1998) with the extension by Kato and Launder (1993) to correct the turbulent-kinetic-energy production near the stagnation point is used to model the effect of turbulence. The extension of Bardina et al. (1985) is used to account for rotational effects. A multi-mode transition model as devised by Kožulović et al. (2007) is used to model transition. Viscous walls in the main flow domain utilize a low-Reynolds formulation of the turbulence model. Walls inside the cavities are not resolved; instead, wall functions are used locally.

To assess convergence, the fluctuating pressure signal at several point probes inside the computational domain is evaluated. Convergence is reached when the maximum amplitude deviation between two periods is below a threshold of Δp=0.1%. Apart from static pressure – which is area-averaged – all flow variables are mass-flow-averaged across the specified planes.

Axial distributions

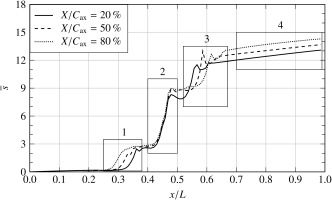
Figure 2 depicts the axial distribution of the circumferentially and spanwise-averaged entropy for all gaps. Four regions of interest are identified:

Figure 2.

Axial distributions of time-averaged entropy (URANS calculations).

Since cavities are not included in the post-processing control volume, entropy fluctuations at the cavity inlets and outlets can be observed, which can also result in a local entropy decrease in the main flow domain. Generally speaking, the entropy increase is steepest in the rotor and stator passages, whereas it is less pronounced outside of the blading. Minimum system loss occurs for the smallest axial gap, while the losses are highest for the largest gap examined. The underlying physical effects are investigated below in further detail.

Two-dimensional flow field

For the quasi two-dimensional flow field at the mid-span, profile losses are the dominant factor. Instantaneous entropy contours at different time steps are pictured in Figure 3 to visualize the wakes for the small and large gaps. The low-momentum wakes of the first stator enter the rotor, experience dilation and are transported into the second stator frame. Because of the comparatively high turning, an increase in axial gap affects the wake mixing process disproportionately. For the large axial gap, the wake is almost entirely mixed out when entering the rotor, the same is true for the rotor wakes entering the second stator. For the small gap, wakes are deflected by the leading edge of the downstream row almost as soon as they are shed: A strong interaction of the wake with the potential field of the downstream row can be inferred. Downstream of the second stator, a highly unsteady flow field can be identified, which is caused by the comparatively strong wake-inducing periodic fluctuations on the suction side: Wakes of varying intensity are shed. As a result, entropy production at the mid-span increases considerably for the smallest axial gap. This evaluation is consistent with the two-dimensional prediction of Praisner et al. (2006).

Figure 3.

Instantaneous entropy contours at mid-span (URANS).

Three-dimensional flow field

The essential aspects of the three-dimensional flow field in the form of circumferentially averaged flow variables were presented by Henke et al. (2016). Figure 4 depicts distributions of streamwise vorticity in measurement plane (MP) 12. With the distance between rotor trailing edge and MP12 remaining constant despite gap variation, both gaps show only minor differences regarding secondary flow, represented here by the streamwise vorticity and the streamwise loss component sSW. The circumferential extent of the hub passage vortex increases slightly for the large gap case, reflecting its dependency on the upstream flow conditions. Regarding wake-related losses in the mid-span region, as represented by the crosswise loss component sCW, a slight increase is found for the medium gap. This is due to the smaller axial gaps increasing the wake interaction between the upstream stator and the rotor, as is also evident in Figure 3. This results in an entropy increase being transported downstream by the wake. The functional decomposition of entropy using the streamwise and crosswise vorticities is capable of identifying individual sources of loss. The hub and tip wall boundary layers are captured using sCW. In the presence of trailing shed vortices, an overlap of both contributions exists in the wake region. An interaction between the vortices and the wakes can be inferred, as the streamwise loss component virtually cuts into the crosswise-dominated region. The presence of sSW in the tip region is a result of shroud leakage flow re-entering the main flow.

Figure 4.

Time-averaged flow field downstream of the rotor (MP12, URANS). Dash-dotted lines denote s_CW; solid lines s_SW.

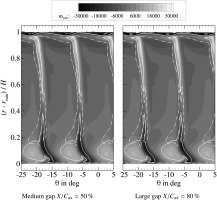
Figure 5 depicts the distribution of the circumferentially averaged streamwise vorticity downstream of the second stator. Additionally, a single contour line of the loss contribution sCW,r, representing the crosswise loss component not aligned in the radial direction, is shown. Naturally, sCW,r is non-zero at the end walls, allowing for the identification of end-wall boundary layer related losses. Of particular relevance is the shear layer caused by the cavity-main-flow interaction at the hub, which merges with the boundary layer and is identified as the main driver for the end-wall losses. End-wall-related losses therefore increase with gap size and the hub-related contribution is higher than the tip-related contribution. Despite sCW,r being, by definition, equal to zero if the local vorticity vector is oriented in radial direction – as is the case for ideal, two-dimensional profile boundary layers and wakes – a non-zero contribution of this fraction can be identified in the mid-span region.

Figure 5.

Circumferentially and time-averaged streamwise vorticity downstream of stator 2 featuring loss contribution s_CW,⌝r (URANS).

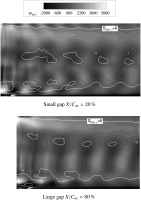
Additional spots of increased sCW,r are visible in the lower third just adjacent to the hub-wall boundary layer. Here, the wakes interacting with the vortices result in vortex deflection where the vortices are virtually cut by the passing wake, as mentioned before. This causes a torsion of the wake, which is the reason behind the non-zero contribution of sCW,r outside of the boundary layers. This effect is more pronounced for the smallest axial gap. As can be seen in Figure 3, the flow area influenced by the wake is much larger for the small gap as a result of the highly unsteady wake shedding at the second stator which exceedingly amplifies wake torsion and resulting vortex deflection. The spots of increased sCW,r near the hub merge with the hub boundary layer into one continuous flow region. This impedes a clear distinction between both individual effects. The blanking merely based on the radial distance to the end walls reveals potential for improvement of the loss decomposition proposed.

Loss analysis

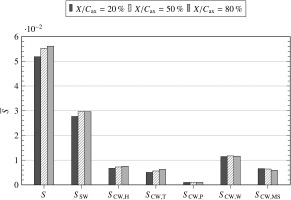
Based upon the detailed flow analysis, losses are broken down in Figure 6. The present study shows that the total system loss increases with the axial-gap size. These results are consistent with Yamada et al. (2009), who investigated a similar turbine configuration. In the hub and tip regions, more pronounced boundary and shear layers from the cavity interaction increase losses for larger gaps. As is evident in Figure 5, the end-wall losses at the hub are higher than at the tip which is also reflected in Figure 6. The profile losses, i.e., the losses immediately caused by the blade boundary layers, are a negligible loss factor and remain almost constant regardless of the axial gap. Interestingly, wake losses also show little variation for a change in axial-gap size. As can be seen in the efficiency distribution in Figure 7, a greater flow-path length between the stator 2 trailing edge and the outlet – which results from a decrease in axial-gap size – leads to an increasing redistribution of total enthalpy from the mid-span into the end-wall regions. This effect is superposed by the aforementioned merging of the end-wall boundary layer and wake structures. Since wake-torsion losses are only accounted for between 15% and 90% of the channel height, as per the definition above, a redistribution into the boundary layers results in an underestimation of the wake-induced losses, i.e., wake losses are counted as end-wall losses in the loss decomposition proposed. This is due to the end-wall and wake-torsion losses being both represented by sCW,r. A closer look at the wake losses at the mid-span between 40% and 70% of the channel height, which are labelled SCW,MS in Figure 6, reveals an increase in wake-induced losses inversely proportional to the axial gap; this is consistent with the observed increase in sCW,⌝r in the mid-span region (Figure 5) and the efficiency distribution in Figure 7. The exact cut-off between the end-wall and mid-span regions as well as the distinction between inter-merged effects can be improved for a better loss prediction.

Figure 6.

Loss contributions from time-averaged URANS.

Figure 7.

Circumferentially and time-averaged outlet flow field for axial gaps investigated.

The losses observed in the mid-span region can be subdivided into direct wake-blade interaction, mixing losses and wake torsion with resulting vortex deflection downstream of the blades. As shown in Figure 3, the maximum increase in entropy actually occurs downstream of stator 2 and not inside of the blade passages, leading to the conclusion that the latter two effects are dominant with regard to wake losses.

The nearly identical secondary-flow losses for the medium and large axial gap suggest that the small axial gap inhibits the formation of secondary-flow-vortex structures disproportionally. If the gap reaches a certain threshold, the secondary-flow losses remain mostly constant, the effect of the increased flow-path length is reflected in the end-wall boundary layer losses. Considering Figure 5 and the decomposition above, it can be argued that the increase in secondary-flow losses occurs primarily in the tip region downstream of the second stator. For the investigated aspect ratio and operating conditions, end-wall related losses (secondary flow and end-wall boundary layers) account for roughly 2/3 of the total losses.

System efficiency

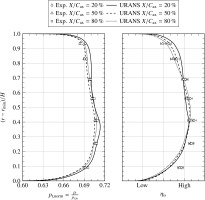
Figure 7 depicts the flow field at the outlet of the control volume for all axial gaps investigated. Of note is the missing total-pressure measurement at 93% of the channel height for the large gap. As the total-pressure information is missing for 2 circumferential positions, no representative average can be calculated at this position. Because of this, and a similar error for the total temperature measurement at 9% of the channel height, no efficiency information at these positions can be given for the large-gap case. For the isentropic efficiency, a clear distinction of the axial-gap size effect depending on radial location can be identified in accordance with the loss breakdown presented: In the hub and tip regions, losses increase for larger gaps. While the hub region shows higher losses in general, the variation, i.e., the influence of the axial-gap size, is higher in the tip region than at the hub. In the region between 40% and 70% of the channel height an inverse trend can be identified, i.e., losses increase for smaller gaps. Of particular note is the aforementioned redistribution from the mid-span region towards the end-wall regions. The small-gap distributions are, therefore, more uniform compared to the larger gaps. The trends discussed apply to both numerical and experimental data although different predictive trends exist at some radial positions. While the good agreement in the total pressure distribution validates the loss breakdown above, the comparatively high measurement uncertainty, however, precludes a detailed assessment of the experimental efficiency distribution.

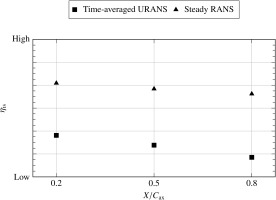
The resulting system efficiency is depicted in Figure 8. In addition to the URANS simulations, results from steady-state calculations are also considered. Despite steady-state CFD not capturing stator-rotor interaction, the overall trend does agree: The smallest gap investigated represents the optimum configuration.

Figure 8.

Total-to-total system efficiency.