Introduction
Turbomachinery blades are susceptible to non-uniform flows generated by inlet distortions, wakes and upstream and downstream pressure disturbances from adjacent blade rows. Pressure non-uniformity is particularly strong in the fan bypass duct due to the existence of pylons and struts which support the fan casing. The potential field disturbances of these obstacles in the form of a circumferentially varying pressure can result in forced excitation of the fan rotor, noise generation and increased aerodynamic losses. These pressure waves can eventually propagate upstream through the fan, and as a result, rotor blades are subject to unsteady fluctuations causing the fan to operate with a non-uniform exit pressure. Operation in a distorted flow-field also affects fan performances.
Analytical models were used for the rotor and stator rows by some researchers (Kodama, 1985) used a two-dimensional compressible semi-actuator disk model based on the theory of small perturbations for a fan stage. Static pressure disturbances due to downstream pylons or struts were separately obtained and imposed at the exit of the fan stage model. However, time-accurate CFD simulations are frequently used in design-optimization systems and are becoming more and more widespread within the industry (Rife et al., 2018; Di Mare et al., 2019). Since the mechanism of rotor interaction with a downstream potential pressure field is inherently unsteady, URANS analyses of a 360° full computational model of the whole stage with downstream obstructions is required to correctly resolve the problem (Enoki et al., 2013) performed three-dimensional unsteady viscous analyses for two fan rotor-stator-pylon configurations with different axial gaps between the stator and the pylon, and compared their results with experimental data. The common characteristic of these numerical strategies based on URANS simulations is their high computational cost. Modeling the aerodynamic effects using full-annulus transient simulations though feasible (Shahpar et al., 2003; Oishi et al., 2012), is still too expensive for routinely used in design offices.
Turbomachinery flows are characterized by their spatial cyclic symmetry and numerical methods taking advantage of it have been proposed to reduce their complexity and cost. Many problems of interest are characterized by two distinctive separate scales and a large multiplicity of similar small-scale elements. In a block-spectral approach, the global domain is decomposed into a large number of similar small blocks making use of scale-dependent solvability. The use of spatial Fourier methods for the computation of nonlinear flows in turbomachinery was first proposed by He (2006). In his original work, He used a block decomposition to study the steady 2D interaction between a fan OGV and a Pylon. Moreover, simplified unsteady cases with two-dimensional (He, 2006) or axisymmetric rotor disk cavities (He, 2011b) were expanded in spatial Fourier series and subject to long-wavelength unsteady perturbations showing good agreement between the spectral method and the full annulus solutions with significant computational savings. He applied the same idea to film cooling configurations (He, 2011a), dimples (He, 2013a) and lined acoustic intakes (He, 2013b). Recently (He, 2018), also extended the methodology to unsteady flows of short temporal and spatial scales (e.g. those due to self-excited unsteady vortices and turbulence disturbances), where a source term-based approach was adopted to facilitate a two-way coupling in terms of time-averaged flow solutions. The present work exploits the same idea extending and applying the spatial Fourier modeling to 3D non-axisymmetric unsteady airfoil passages under the presence of long-wavelength flow instabilities without making any explicit assumption about the temporal periodicity of the flow.
A time-marching Passage-Spectral Method (PSM) is proposed in this study to reduce the computational cost of these unsteady and non-axisymmetric simulations and simplify the study of the fan rotor stability under the effect of a distorted exit static pressure without making any hypothesis about its temporal periodicity. The idea is essentially the same presented by He (2006). The Passage-Spectral naming is solely used a means of highlighting that the blocks coincide with the blade passages. This approach, which has been verified against full-annulus cases for rotating stall and force response cases in an isolated fan-stage (Romera and Corral, 2020a), has been further modified to deal efficiently with a single spatial harmonic and then applied to assess the effect of inlet distortion on fan stability (Romera and Corral, 2020b). Despite the number of struts or pylons and their geometrical complexity, any outlet static pressure distortion pattern can be Fourier decomposed. The stability of the spatial harmonics content can the be assessed separately using the proposed PSM filtering the contribution of the rest of the circumferential modes of the downstream perturbation. The validity of this approach has been shown by (Romera and Corral, 2020b). In this model, just three reduced-passages are retained. The proposed method assumes that the circumferential wavelength of the potential disturbances is much larger than the blade spacing. In this paper first, the nonlinear stability of each nodal diameter at the outlet is investigated as a function of the perturbation amplitude taking advantage of the use of the novel method. Next, full-annulus simulations are carried out to increase the credibility of the stability maps. In the authors’ opinion, this is the first time clear conclusions are drawn about the influence of the outlet distortion shape on fan stability.
Numerical setup
The baseline solver, known as
The existing parallel CFD code was modified and customized for this work to study the contribution of a given single spatial harmonic M efficiently, by approximating the solution with only three reduced-passages samples spanning over a sector of size
The code is based on the virtual existence of a Fourier transformation of the homologous nodes of the different passages,
where
being
Figure 1.
Schematic of a sinusoidal distribution in full-annulus (left) and its approximation (right) with three reduced-passages samples (dark grey) uniformly spaced.

Once the solution of the three uniformly spaced reduced-passages is calculated at each time step (see Figure 1), the reconstructed full-annulus solution can be obtained Fourier decomposing the flow variables at all the nodes of the sample passages. Once the Fourier coefficients at all the nodes of the passage are obtained these can be used to expand the solution to the full circumference. Since the reduced-passage samples play the role of sampling points for the circumferential Fourier transform and require uniform spacing, the circumferential location of these sample passages does not correspond in general with the position in the full-annulus of the physical blades or passages. The Fourier coefficients use as reference the first reduced-passage (
Fan stability
This section aims at studying the nonlinear aerodynamic stability of a generic fan blade operating at a constant speed under the potential effect caused by a circumferential distribution of static pressure at the outlet, which is parameterized in terms of its nodal diameter and static pressure amplitude. The performances and stability of axial flow fans and compressors is affected by the circumferential variations in exit static pressure produced by thick struts or other components if they are not located far enough from the fan rotor. These flow disturbances are usually dominated by long circumferential wave-lengths (i.e. much longer than the blade pitch) which makes the Passage-Spectral Method well suited for their analysis since it avoids the use of full-annulus simulations. Moreover, the method allows investigating the independent contribution of the different NDs efficiently. It is important to point out that this is not the case in nonlinear full-annulus simulations since when the perturbations are large, and the linear stability regime is by-passed, the nonlinear interaction amongst the different NDs is unavoidable.
In this regard, the method has been adapted to simulate an arbitrary single ND perturbation, simulating the equivalent effect of different number of pylons downstream, using solely three reduced passages to fit the desired wave-length over a sector of
Numerical set-up
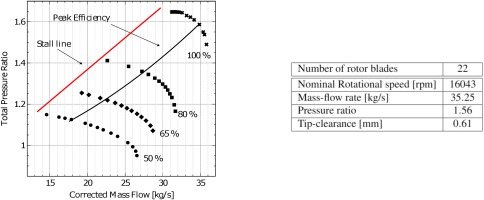
The NASA rotor 67, which is a low-aspect-ratio fan with 22 rotor blades, has been chosen as the test vehicle. Figure 2 summarizes the fan design parameters at 100% of the design speed. The rotor blade is discretized using a semi-structured grid (Burgos et al., 2011). Firstly, a hybrid grid in the blade-to-blade plane with 118 points around the airfoil and 24 quad layers in the boundary layer has been constructed. Next 151 layers in the span-wise direction are extruded. To resolve the tip leakage flow 6 mesh layers were included between the blade tip and the casing. The final grid consists of about
One-dimensional non-reflecting boundary conditions were imposed at the inlet and the outlet. At the exit, the radial equilibrium equation was applied to fix the pressure radial distribution. Non-slip and adiabatic wall boundary conditions were applied to the blade surfaces and the inner and outer casing walls. The Reynolds number of the simulations is very high
The mass flow evolution for three different time resolution (200, 400 and 4,000 time steps/rev) has been analyzed. We concluded that 400 time steps per rotor revolution is sufficient to predict the stall margin. It should also worth mentioning that the stall margin is greatly influenced by the size of the time step (Zhang and Vahdati, 2017). The use of a large time steps over-predicts the stall margin, delaying the stall inception at a given mass flow of reference. Just to conclude, unsteady simulations have been conducted using 400 time steps per rotor revolution. A previous analysis was also done for the number of pseudo time steps per physical time step, fixed to 60, which is large enough to achieve the convergence criterion of the inner iteration of the dual time step. The base flow is uniform and axial at the outlet, but the static pressure is modified circumferentially by superimposing an arbitrary Fourier series but keeping the radial distribution of the static pressure.
Stability map
This section aims at studying the influence of downstream circumferential static pressure patterns on fan stability to shed some light on the influence of the pylon shape and number off in the non-linear stability of a fan-stage. A computationally efficient method is used to enable this analysis during the conceptual design phase of the fan. The nonlinear stability of the fan is then investigated in a nodal diameter basis retaining the spatial harmonic corresponding to the outlet static pressure perturbation solely. The pressure ratio is modified by changing the mean level of the circumferentially average exit static pressure.
The effect of circumferentially varying the amplitude of the outlet static pressure for the first four nodal diameter patterns on the fan stability is investigated with the Passage-Spectral Method at
The study of the amplitude effect of a static pressure perturbation downstream on the fan has been carried out taking into account realistic circumferential patterns previously reported in the literature. (Enoki et al., 2013) conducted aerodynamic and acoustic tests for a transonic fan stage with a simulated top pylon. The potential pressure field that was created by the engine pylon was about 15% of the mean static pressure three chords downstream from the fan. Taking into account the actual static pressure at the outlet of the simulations carried out at the aerodynamic design point, the amplitude of the static pressure perturbation at the exit has been varied between
The nonlinear stability maps for the first four NDs computed with the PSM are shown in Figure 4. The unstable regions are shaded in color. The blue circle with the minimum mass-flow coincides with the last converged point with the single-passage steady version of the solver. At this OP the fan is unstable under infinitely small perturbations. As the mass-flow is increased the fan is more tolerant of outlet perturbations. The stability of the first and third NDs, see Figure 4a and c, are practically not altered by the perturbation level. These cases exhibit nearly straight vertical lines departing from the same point, at least within the error of the method, which is the linear or small perturbation stability limit. This instability process is nonlinear, since the perturbations have finite amplitude, and for small perturbations, this phenomenon cannot be seen. Its simulation requires of fully nonlinear analyses.
Figure 4.
Stability conceptual map due to different amplitudes of static pressure patterns at the outlet and nodal diameters using the PSM just retaining the harmonic M = N D N D = 1 N D = 2 N D = 3 N D = 4
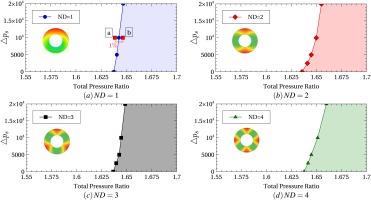
It can be seen that the contribution of the different NDs to nonlinear stability is qualitatively different. The most surprising result of Figure 4 is the stabilizing behavior of
The stability of the fan-stage under small perturbations is studied next. The simulations are set with a constant circumferentially uniform static pressure at the exit (
This type of plot is difficult to construct using full-annulus simulations, especially if the stability limit of the different modes is similar in the parameter space since it is difficult to control and track the development of the different unstable NDs when they are active simultaneously in a single simulation. However, Figure 4 suggests that if high enough perturbations with
It is illustrative to compare these results with the more classical problem of intake distortion where a total pressure defect is set at the inlet. This problem has been addressed as well by (Romera and Corral, 2020b) using the NASA rotor 67 fan as well and following the same approach. In that case, the
Validation and results
Full-annulus simulations have been conducted aiming not only at validating the results obtained in the previous section but also to show the transient behavior when the flow-field becomes unstable. Steady solutions at 100% of the design speed with uniform outlet static pressure are used as the initial solution for the unsteady simulations. The full-annulus solutions obtained for the points marked as a and b in Figure 4a are discussed next. These two OPs have a slightly different pressure ratio,
Figure 5a compares the mass-flow time evolution during the first 20 revolutions at the rotor inlet for the operating points a and b, corresponding to pressure ratios of
Figure 5.
Full-annulus comparison between stable and unstable conditions with a first nodal diameter ( N D = 1 ) Δ p s = 10 , 000 Pa P R = 1.64 P R = 1.65 1 s t ( m = 1 ) Δ p s
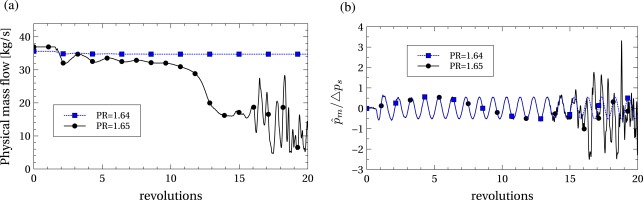
Figure 5b displays the time evolution of the first circumferential harmonic
After approximately 15 rotor revolutions, the first harmonic of the static pressure at the numerical probe located downstream of the fan blade is triggered and experiences rapid exponential-like growth, as shown in Figure 5b, which indicates a rapid development of the non-axisymmetric flow in this region. Once the stall process is triggered, the first harmonic
Computational efficiency
The speedup factor,
Conclusions
Unsteady simulations have been carried out for the NASA rotor 67 fan blade to investigate its aerodynamic stability under the effect of potential disturbances induced by pylons and struts located downstream of the fan. The reduced-order Passage Spectral Method and full-annulus representations of the fan have been used. The PSM has been slightly modified aiming at efficiently handling outlet static pressure distortion in a nodal diameter by nodal diameter basis filtering the nonlinear contribution of the rest of the nodal diameters.
The proposed methodology is based on the heuristic assumption that the spatial harmonics of the outlet static pressure perturbations can be Fourier decomposed and evolve independently, even in the nonlinear stability regime. However, the method makes no hypothesis about the interaction between the different spatial modes. The method is fully nonlinear. In this case, independent nonlinear stability maps for each nodal diameter can be constructed. The presence of second and fourth nodal diameters has a nonlinear stabilizing effect on the fan rotor blades. The stability of the fan is not altered by the presence of finite-amplitude first and third nodal diameter perturbations. The stability threshold for one of the distorted static pressure patterns has been assessed using full-annulus simulations. The error has been estimated at about 1% in terms of total pressure ratio. This conclusion has been derived using an iterative procedure involving full-annulus solutions. If just the four first NDs are computed using the PSM this analysis can be conducted overnight in a modest cluster with 16 GTX 1080ti GPUs with a significant reduction in computational resources with respect to full-annulus analyses.