Introduction
Film cooling is a method which is essential in gas turbine engines to mitigate the adverse effects of high temperatures on turbine components. This improves the thermal efficiency of the engine and durability. Understanding the complex aerodynamic and thermal phenomena associated with film cooling is critical for advancing turbine design and optimization. Despite the extensive research conducted over the last 50 years, including fundamental work such as Goldstein’s (1971), a complete understanding of the flow physics remains elusive, primarily due to the large number of influencing factors, such as geometric configurations and flow parameters.
Many studies focus on flat plates and low temperatures
Very few test rigs are currently able to generate comparable test conditions. In the 1980s, turbine blade measurements were carried out at temperatures of up to
Methodology
Experimental setup
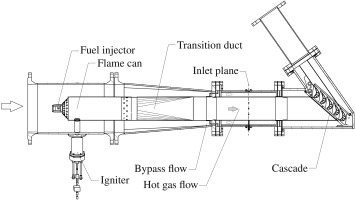
The Linear High-Temperature Cascade (LHTC) at the Institute of Jet Propulsion and Turbomachinery is a test rig designed to test cooled turbine blades at high temperatures and realistic density ratios (Findeisen et al., 2017). Currently, the rig is being used to test and validate film-cooled turbine blades as part of a research project. The rig can operate at main flow temperatures of up to
where L is the chord length, A the cross section area of the inlet section and
Blade configuration and instrumentation
The cascade is comprised of five blades, of which the outer blades form the wall for the hot air flow, while the three blades in the middle of the cascade are used for temperature (middle blade) and pressure measurements (adjacent blades), cf. Figure 2. The blade cooling design is derived from the mid-section of a high-pressure turbine blade and features four smooth internal cooling channels. The three middle blades each have 18 cylindrical film cooling holes which are located on the suction side of the first channel. To ensure mass conservation in the fourth channel, trailing edge ejection is not utilized. The blades are mounted in the test rig with the tip plates facing downwards. The middle blade is equipped with a total of 66 thermocouples to measure the metal temperature of the blade. Of these, 32 thermocouples are located in the mid-plane, while 16 thermocouples are located in both the hub and tip planes at 10% and 90% of the blade height respectively.
Figure 2.
Test blades with measurement locations. (a) Mid-section of the tested blade showing the cooling channels and the location of the film cooling row with 18 cylindrical film cooling holes at s / L ≈ 0.35
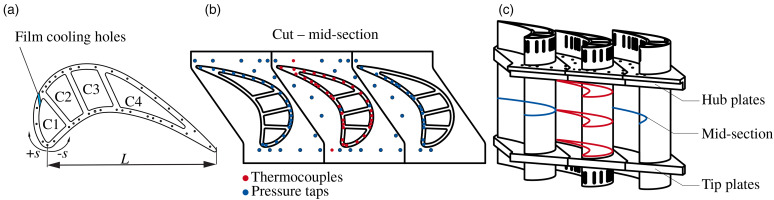
The blades to the left and right of the center are used for measuring the profile pressure at a total of 37 pressure taps. Based on the profile pressure the isentropic Mach number
is calculated, where pt,HG is the main flow total pressure at the inlet plane and
Blade cooling
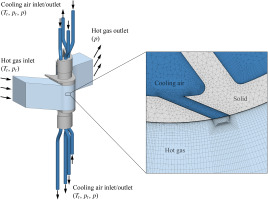
The cooling air is provided by a separate compressor and can be heated by a flow heater to up to 573 K. A total of six valves are used to control the mass flow to the blades. Figure 3 shows the cooling air supply and tubing for the central blade. Air is supplied to the entrance of channels 1 and 2 from the flow heater. Instead of using the usual internal deflection, the cooling air is guided out of the blade and deflected to a pipe section before entering the next cooling channel. After passing channel 1, the cooling air is blown out into the bypass flow. The cooling air from channel 2 is guided through pipes outside the blade and redirected into the following channels 3 and 4. Downstream of channel 4, the cooling air is blown out into the bypass.
Figure 3.
External cooling air pipes of the central measurement blade, (a) top side and (b) bottom side of the blade. Static pressure, total pressure and temperature are measured at each channel inlet and outlet.
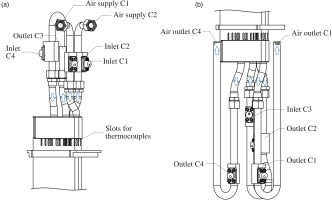
To characterize the cooling air flow, cooling air measurement sections (CAM) are used. Six CAMs are placed at the cooling air inlets of the three middle blades, so that each inlet is measured separately. Six more CAMs are placed in the external cooling air path of the middle blade (cf. Figure 3), so that there is one measurement section upstream and downstream of each channel respectively. This enables the measurement of inlet and outlet quantities at each of the four cooling air channels of the center blade. These values serve as boundary conditions for CFD calculations of the blade.
Each CAM contains a combined Kiel head probe for total pressure and total temperature measurements (cf. Findeisen et al., 2017). Additionally, three pneumatically averaged static pressure taps are located upstream of the Kiel probe to determine the Mach number, which is used for recovery factor correction of the total temperature probe. The coolant mass flow
The operating point of the cooling air is determined by the combination of coolant temperature
The film cooling mass flow
is used, where
Numerical setup
Steady-state conjugate heat transfer (CHT) simulations were performed to analyze both the aerodynamic characteristics and the thermal conditions of the blades. The numerical setup shown in Figure 4 is composed of the hot gas domain, the cooling air domain and the solid blade domain. Separate computational meshes were created for each domain using Ansys ICEM CFD. Ansys CFX was used for all steady-state simulations. The hot gas domain featured only one passage of the test rig with periodic boundaries in pitchwise direction. At the inlet, total temperature and total pressure profiles from the inlet probes were used. Since there is no pressure measurement downstream of the cascade, the outlet static pressure was adjusted to match the blade surface pressure distribution of the experimental data. The hot gas was modeled as an exhaust gas consisting of
The solid domain is placed between the hot gas and the cooling air. The thermal conductivity of the solid matches the properties of Alloy X. Fluid-solid interfaces are defined on the walls adjacent to the hot gas or cooling air flow respectively. All walls located within the bypass are almost adiabatic due to the thermal insulation in the test rig.
All simulations were carried out using both the
Based on the simulation results, the momentum ratio I of the film cooling flow can be calculated
The momentum of the main flow
Results and discussion
In this section, we first present the measurements of the inlet plane, which serve as inlet boundary conditions for the simulation. Next, we provide the experimental results obtained for a main stream temperature of
Table 1.
Experimental operating points.
| OP | ReHG | Tt,HG | DR | MR | TCRa | Ib |
|---|---|---|---|---|---|---|
| 1 | – | |||||
| 2 | ||||||
| 3 | – |
Inlet conditions
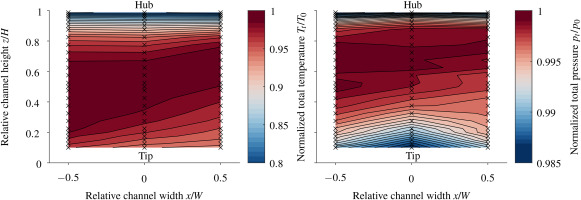
The inlet profile of the main flow for the following results is shown in Figure 5. The temperature profile at the inlet shows a significant gradient in the vertical direction (z), with temperature peaks located above the channel mid-plane. A thermal boundary layer is visible near the hub. The total pressure near the tip is significantly lower than at the hub, which can be explained by the interaction between the rotation-symmetric temperature profile generated by the fuel nozzle of the flame can and the liner. The transition duct changes the circular cross-section of the combustor the rectangular shape of the inlet section. This transition involves a reduction in channel height to half the diameter of the combustor section, while maintaining a consistent channel width, which results in the following two effects. First, the rotation-symmetric temperature profile contracts vertically. Second, the resulting non-uniform flow acceleration induces a secondary flow that transports cold fluid from the near wall towards the hot gas mid-plane (Mick et al., 2013). These overlapping effects explain the observed total temperature and pressure profile, which remains consistent for all operating points.
Validation of the CFD results
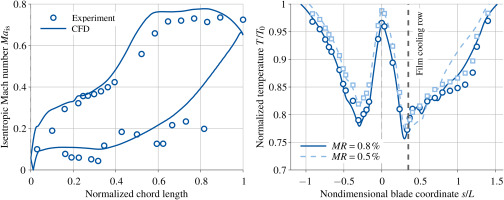
CFD simulations were used to get a more detailed view of the flow field and the heat transfer of the blade. A comparison between the experimental data and the numerical results is shown in Figure 6. The left-hand diagram illustrates the isentropic Mach number
Experimental results
Effect of varying coolant mass flow ratio
Figure 7 shows on the left-hand side the normalized blade temperature of the film-cooled blade for four different mass flow ratios. As the coolant mass flow increases, the material temperature generally decreases due to the higher overall cooling air flow. This effect is particularly noticeable on the pressure side which is only convectively cooled and on the suction side upstream of the film cooling row. The design of the blade causes film cooling and convective cooling to interact. A high film cooling mass flow requires high pressure in the cooling channels due to the significant pressure loss at the exit of the film cooling holes. However, the pressure resistance for the internal cooling flow, which determines the mass flow, remains almost constant. The total mass flow therefore increases disproportionately when
Figure 7.
Normalized material temperature at the mid-section plan for different coolant mass ratios MR DR
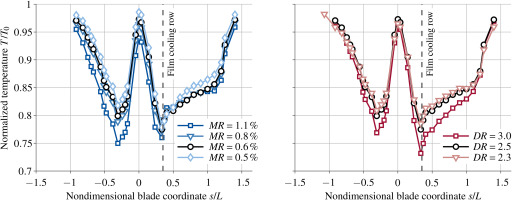
Downstream of the film cooling holes
Effect of varying density ratio
In the right-hand diagram of Figure 7, the coolant mass flow ratio is held constant
Improvements in effectiveness due to film cooling
In the following section, we use CFD simulations to distinguish between the influence of film cooling and convective cooling respectively. For the evaluation of a convectively cooled reference blade, the mass flow through the film cooling holes is set to zero. Then the cooling is evaluated on the basis of the overall cooling effectiveness
where
is used. Figure 8 illustrates the difference in overall cooling effectiveness at comparable boundary conditions for different coolant mass ratios
Figure 8.
Cooling effectiveness difference Δ ε
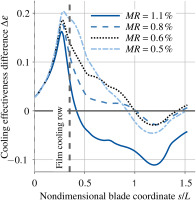
As expected, there is a notable improvement in cooling effectiveness downstream of the film cooling holes in the first region. When the momentum ratio increases however, the improvement gets smaller until the delta effectiveness becomes negative at very high momentum ratios, signifying that the temperature is higher than for the only convectively cooled blade. It is likely that this occurs as a result of the detachment of the cooling jet, which allows hot gas to reach the blade surface and increases the heat transfer coefficient on the blade surface.
Figure 9 shows contours of the cooling air mass fraction in order to visualize the propagation and structure of the film cooling jet entering the external flow. For the higher momentum ratio of
Figure 9.
Cooling air mass fraction of the film cooling jets in the middle plane at two positions perpendicular to the jet at two different MR
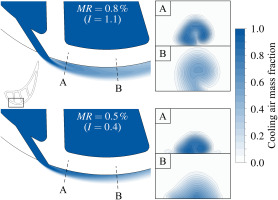
In the intermediate region, the effects are more complicated. The reference mass flow ratio
In the mixed-out region, no significant improvement can be observed. For high and low
Conclusion
This work investigates a film-cooled turbine blade in a high-temperature environment of
In the future, we aim to validate these findings experimentally. To achieve this, we plan to measure a blade of the same design that is cooled solely by convection. This will allow us to identify more precisely the effects which are related to film cooling. On this basis, we aim to investigate the superposition effects of multiple film cooling rows by gradually adding more rows on the suction and pressure sides.
Nomenclature
Latin symbols
Cross section area (m2)
Speed of sound (m/s)
Density ratio
Momentum flux ratio (−)
Chord length (m)
Mass flow (kg/s)
Mach number (−)
Coolant mass ratio
Pressure (Pa)
Specific gas constant (J/(kgK))
Reynolds number (−)
Blade coordinate (m)
Temperature (K)
Total coolant ratio (−)